• home
• about
• new
• essays
• AI
• book

Peter Collins is from Ireland. He retired recently from lecturing in Economics at the Dublin Institute of Technology. Over the past 50 years he has become increasingly convinced that a truly seismic shift in understanding with respect to Mathematics and its related sciences is now urgently required in our culture. In this context, these present articles convey a brief summary of some of his recent findings with respect to the utterly unexpected nature of the number system.

The Remarkable
Euler Formula

Part I: Limits of Interpretation

Peter Collins

Introduction

I read Andrew Smith's review of “The Mathematical Universe” [Getting to the Point] (and Elliot Benjamin's reply [The Mathematical Universe, Science and Euler's Formula]) with much interest.

As the worldview of the author Mike Hockney (apparently a pseudonym for a secret member of a Neo-Pythagorean group) is centred to a considerable extent on the Euler formula, I thought that it might be of interest to focus specifically on this remarkable relationship, the true significance of which greatly transcends what can be understood within the accepted analytic framework of Mathematics.

There is widespread agreement within mathematical circles regarding both the importance and beauty of the Euler formula (also referred to as the Euler identity, equation, theorem etc.) [1]

The great physicist Richard Feynman esteemed for his frank no-nonsense type brilliance called the Euler formula “our jewel” and "one of the most remarkable, almost astounding, formulas in all of mathematics."

The mathematical biographer Constance Reid referred to it as “the most famous formula in all of Mathematics”.

Paul Nahin the mathematician and author of a comprehensive book on Euler's formula and its important applications to Fourier analysis, states that it sets “the gold standard for mathematical beauty”.

And a poll of readers conducted by the Mathematical Intelligencer in 1988, named Euler's formula as “the most beautiful theorem in mathematics”.

Then in a later poll in 2004 conducted by Physics World, it tied with Maxwell's equations of electromagnetism as “the greatest equation ever”.

Just think about this for a moment! Here was a poll conducted among physicists. Yet Euler's equation, a purely mathematical construct, was ranked ahead of Einstein's famous equation E = MC²! The reason for this is due to the many highly important applications the formula has in physics.

However a clear indication, that the true meaning of the Euler formula transcends conventional mathematical understanding, is evident from the following two quotes, the first of which relates to Benjamin Pierce who after demonstrating the proof declared:

"it is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth."

And Keith Devlin, in a wonderfully poetic manner, not normally associated with mathematicians has stated:

"Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence."

Thus it is my intention in these articles to highlight that not alone can the Euler formula be given the standard analytic (Type 1) but equally a compelling holistic (Type 2) mathematical interpretation (for which no formal recognition yet exists).

Even more importantly, I contend that the true significance of the equation can only be properly understood as the highly refined experiential interaction of both aspects.

In fact at its deepest level of comprehension, the Euler formula conveys the most original mathematical meaning humanly possible in the direct coincidence of both the analytic and holistic type understanding of its symbols.

Brief History of Formula

Though generally in human thought, an important discovery comes to be exclusively associated with one person, this in fact is rarely the case.

For example the famous equation E = MC², already mentioned, establishing the equivalence of mass and energy, is universally associated in the popular mind with Einstein.

However it has been claimed that an obscure Italian industrialist, Olinto de Pretto, [2] published the equation in a scientific magazine in 1903 and furthermore that Einstein was aware of this finding. However de Pretto, who did not understand Relativity, lacked the context to fully appreciate the significance of the equation he had published. So the credit for the discovery and the consequent fame went to Einstein.

It is somewhat similar in relation to the Euler identity.

One well-known form (as Andy indicated in his article) is given by the equation,

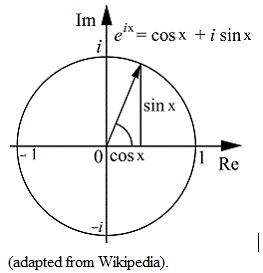
e^ ix = cos x + i sin x. [3]

Roger Cotes, who was a close associate of Isaac Newton, discovered an equivalent form of this expression in 1714,

i.e. ln (cos x + i sin x) = ix. [4]

As this expression is based on the natural logarithm e, it directly implies that e ^ ix = cos x + i sin x.

The French mathematician de Moivre, who was highly esteemed by Newton, discovered an important extension of this result in 1722,

i.e. (cos x + i sin x) ^ n = cos nx + i sin nx (known as de Moivre's Theorem).

Then around 1740, Euler gave extensive consideration to the relationship, through examination of the exponential function and arrived at this result without the use of logarithms,

i.e. e ^ ix = cos x + i sin x.

He also was the first to discover a simple transformation, which leads directly to the most remarkable expression of the relationship, giving it the form by which it is now generally known.

When x in the formula = pi, then,

e ^ (i * pi) = cos pi + i sin pi.

Now pi in this context refers in trigonometric terms to the number of radians. And pi radians = 180 degrees.

Therefore e ^ (i * pi) = cos 180 + i sin 180.

And it can be simply verified on a calculator that cos 180 = – 1, and sin 180 = 0.

Therefore e ^ (i * pi) = – 1 + i(0) = – 1.

Then by a simple rearrangement of the terms in the equation,

e ^ (i * pi) + 1 = 0.

Further developments - which even Euler did not foresee - led to the important realisation that the general case of the formula,

e ^ (ix) = cos x + i sin x,

can be viewed in geometrical terms as tracing out points on the circle (in the complex plane) thereby enabling representation of the various roots of 1.

A beautiful presentation of the Euler identity (including an outline of the proof which is relatively short and simple) can be found here on YouTube:

It provides a powerful connection as between complex analysis (related to number theory) and trigonometry. Andy in his review referred to its highly important application with respect to Fourier transforms. This can then be applied in turn to a wide variety of wave functions in physics, electrical engineering and even pure number theory.

Not surprisingly, it shows up in the most important mathematical problems e.g. the Riemann Hypothesis (relating to the nature of the number system) and The Classification of Groups (relating to the nature of symmetry).

Analytic Interpretation of Formula

The popular form of the relationship,

e ^ (i * pi) + 1 = 0, combines the 5 most important mathematical constants 1, 0, e, i and pi (each once in an extremely economical manner).

It also contains the equality relationships and the fundamental operations of addition, multiplication and exponentiation (again just once). (Indirectly through i, it also contains subtraction).

So in order to gain a better understanding of what is involved here, we will now provide some clarification of these various mathematical symbols.

1 and 0 represent the original - and most important - members of the number system.

The notion of 1 is implicitly involved in the recognition of any phenomenon (as a distinctive unit).

By contrast 0 (as zero) literally represents no-thing.

The relationship as between 1 and 0 is given by the apparently simple relationship,

1 – 1 = 0.

However this raises an immediate problem of the first magnitude.

In the very dynamics of experience, the direct positing of an object as a unit (1) implicitly entails a relationship with nothing (0).

In reverse fashion, the recognition of 0 is likewise dynamic (implying the negation of 1).

For example, if I recognise that there is no money in my account, this can only have meaning with reference to a phenomenal notion of money.

Thus strictly speaking in experiential terms, the very notions of 1 and 0 arise in a dynamic interactive manner and are quantitative and qualitative with respect to each other,

However a reduced quantitative interpretation of both numbers is given in conventional mathematical terms, where they are abstracted from each other in an absolute manner.

I am not questioning for a moment the great value of such reduced interpretation!

As we know, all numbers - indeed potentially all information - can be represented in binary terms through the digits 1 and 0.

So the incredible wonders of the present digital age of information intimately depend on the quantitative representation of 1 and 0 as absolutely separate from each other.

However this interpretation does not accurately reflect the dynamic manner in which number is experienced. So, as we shall see later, from the holistic perspective, both numbers are ultimately seen as identical with each other.

e (2.718281828…) is sometimes known as Euler's number and is the base of the natural logarithmic system.

With the exception of pi, it is the most important transcendental number in Mathematics.

The very term that is used to describe these two numbers suggests that their meaning literally transcends rational understanding!

I will point here to a significant issue regarding all transcendental numbers.

Transcendental in fact represent an extreme version of what are termed irrational numbers.

As is well known, the Pythagoreans recognised that the square root of 2 is irrational.

However this differs from a transcendental number in that its value arises in the context of an algebraic equation.

Thus if x (squared) = 2, then when we solve for x, we obtain the square root of 2.

So the square root of 2 (though irrational) still has a definite connection with the rational world of numbers in the sense that when squared, the number 2 results.

However a transcendental number - by definition - cannot be expressed as the solution to such an equation, making its nature much more elusive. [5]

The problem with transcendental numbers such as e (as indeed with all irrational numbers) is that their quantitative value cannot be precisely known in an absolute manner i.e. cannot be expressed as a rational fraction. Though this is indeed fully recognised, its important philosophical significance is completely overlooked.

In other words, though we may approximate the value of e to any required degree of accuracy (in quantitative terms), its “true” value necessarily remains of an indeterminate nature. In this sense, we have precisely the same problem with respect to the number system that is now accepted as an indelible feature of quantum physical reality.

So an uncertainty principle applies to the value of irrational numbers, which properly reflects the interaction of both (finite) quantitative and infinite (qualitative) aspects in dynamic relationship to each other. This problem is not clearly recognised in conventional mathematical terms, as the infinite itself is misleadingly reduced in a static quantitative manner (as a linear extension of finite notions).

Thus once again, what we are presented with in conventional mathematical terms is but a reduced - merely quantitative - interpretation of a relationship that, properly understood, entails the dynamic interaction of both quantitative (finite) and qualitative (infinite) notions.

There are many expressions for e. The simplest indeed entails viewing it as a dynamic version of 1. So if we increase 1 by a very small fraction 1/n and then raise the sum to the power of n, the result will approximate ever closer to e, as n becomes larger.

In conventional mathematical language, it will then be stated that in the limit, as n approaches infinity, the result = e. But this represents something of a fudge, as “infinite” has no strict meaning approached from a finite perspective. Therefore we, necessarily always remain in the realm of approximation with respect to the “true” value of e (which cannot be absolutely determined in a quantitative manner).

This notion of e has an intimate bearing on financial problems involving the compounding of interest rates.

Imagine first the very fortunate scenario where one is awarded a 100% rate of interest per annum on an investment of €1!

The total value of the investment for the year entails the approximation of (1 + 1/n) ^ n where n = 1.

Therefore at the end of the year, the investment will be (1 + 1) ^ 1 = €2.

Imagine then the situation where the interest is calculated every six months (at 50% interest rate for the period).

This brings in the notion of compound interest, with the rate in the second six months based on the total amount already accumulated in the first period.

This represents our approximation where n = 2,

i.e. (1 + 1/2) ^ 2.

It is easy to verify on a calculator that this = €2.25.

To get closer to the true value of e, let us imagine that interest is compounded on a daily basis.

Then the approximation for the value of the investment will now be,

(1 + 1/365) ^ 365.

Again, it is easy to verify on a calculator that this compounding of interest on a daily basis will lead to the value of the investment at the year's end = €2.71 (approx).

This is indeed much closer to the “true” value of e, i.e. 2.718281828…

So, if we keep compounding interest for increasingly shorter periods of time, the value of our investment at the end of the year will approximate ever closer to the “true” value of e.

Now we can liken this to the refresh rate of a movie projector. As the refresh rate increases, the jerkiness with respect to the quality of the pictures decreases. Thus when the time frame for each “still” is sufficiently short, it becomes difficult to distinguish each discrete frame from the continuous movement of the movie.

Put another way, the differentiation of each frame becomes inseparable from the integration of all frames.

And this is the central reason why e is so important, as it is the only number where the notions of (discrete) differentiation and continuous (integration) can be directly identified with each other (in a relative approximate manner). [6]

However, both differentiation and integration are properly quantitative and qualitative with respect to each other. Therefore once again these notions are necessarily reduced in conventional mathematical terms in a merely quantitative manner.

Now pi is the other especially important transcendental number, perhaps even better known than e. It represents the ratio of the circumference of a circle to its line diameter. However as with e, a central mystery attaches to the nature of pi, which can only be determined in an approximate manner (i.e. 3.14159265...).

So just as 1 and 0 are quantitative and qualitative with respect to each other, the geometrical notions of the line and circle (which are closely related to these two numbers) [7] are likewise properly quantitative and qualitative in terms of each other. So once again a merely reduced quantitative interpretation is offered in conventional mathematics). [8]

In some ways i, which represents the square root of – 1, is the most interesting of these fundamental constants. [9]

Understanding of the modern number system would be simply impossible without the incorporation of i. So present-day Mathematics increasingly requires the use of complex numbers, incorporating both a real and an imaginary part (based on i).

However despite the recognised importance of imaginary numbers in quantitative terms, little or no understanding exists as to their enormous philosophical significance (which implies the corresponding qualitative appreciation).

Putting it simply, interpretation of our world would be dramatically changed through proper understanding of the qualitative nature of imaginary numbers. In fact, as we shall see, imaginary numbers represent the hidden holistic aspect of number (expressed indirectly in analytic terms).

We can however identify the nub of the issue here.

In my articles on the number system, I defined two aspects that are - relatively - quantitative and qualitative with respect to each other.

The real numbers belong to the Type 1 aspect, where they directly concur with quantitative notions of measurement.

So, for example 2, as a real number quantity, is fully expressed as 2 ^ 1.

However i, the basic unit for all imaginary numbers, belongs directly to the Type 2 aspect.

In fact i relates to 1/4 in the Type 2 system (i.e. 1 ^ 1/4) which then can be quantitatively expressed in an indirect circular manner (as the 4th root of 1).

This means that - properly understood - real and imaginary numbers belong to number systems that are quantitative and qualitative with respect to each other.

Therefore when we attempt to treat imaginary numbers (like real) in a merely quantitative manner, great confusion can arise.

For example in complex analysis (involving real and imaginary numbers), mathematicians take considerable comfort from following accepted quantitative procedures. However, a deeper philosophical appreciation of what is involved, that should properly guide such quantitative work, is sorely missing. And this properly comes from holistic - as opposed to analytic – understanding.

This in fact explains well the remark of Benjamin Pierce that we quoted earlier in the article. Though he knew he had proved Euler's identity (because he had followed the accepted quantitative procedures), he then honestly admitted that he had no idea what the result meant! And a key part of the problem here, is the manner in which the imaginary number i appears in the exponent of e.

Indeed this is why the Euler identity seems so mysterious, as Conventional Mathematics is greatly lacking the appropriate holistic intuition to properly appreciate the behaviour of imaginary numbers.

Of course there is an important quantitative role for such numbers. However there is an equally important qualitative role that is still unrecognised. And the true power of imaginary numbers can only be properly unleashed when both aspects are successfully combined with each other.

Though both the real and imaginary aspects of number are now fully accepted from a quantitative perspective in Mathematics, the corresponding need for both real (analytic) and imaginary (holistic) interpretation of such numbers from a qualitative perspective is not at all recognised!

With respect to operations, addition represents the adding of two numbers (e.g. 2 + 3) as opposed to their multiplication (i.e. 2 * 3). Exponentiation arises in the context of successively multiplying by the same number. So 2 * 2 * 2 (where 2 occurs three times would be represented as 2 ^ 3.

However somewhat surprisingly, these apparently simple operations conceal fundamental difficulties which again ultimately derive from the fact that inherently they entail both quantitative and qualitative notions in dynamic relationship with each other.

Unravelling the Formula

Having briefly explained its various components, let us now attempt to unravel what the formula is stating (from an analytic perspective).

Before doing so, I will present here a slightly amended presentation of the Euler identity,

e^ (i * pi) = – 1 .

By squaring both sides we obtain,

e^ (2i * pi) = 1. I refer to this as the fundamental Euler identity (entailing a full - rather than half - circular rotation).

This is really a more natural version of the identity and in the form that customarily shows up in related applications. We also have the additional benefit here of including the number 2 which surely must qualify as the next most important constant (after the 5 mentioned).

We have already explained the notion of e with respect to an investment occurring in linear time (i.e. 1 year).

Thus we used e to calculate the total value of the investment at the end of 1 year. So the time periods for which the investment is calculated become increasingly small, with the corresponding number of time periods becoming increasingly large (both without limit).

This is represented as e ^ 1.

In like manner, if we wanted the value of the investment for 2, 3,…n years, we would calculate e ^ 2, e ^ 3,…… e ^ n respectively. For example after two years the total investment would be worth €7.39 (approx).

So again, this clearly conveys the notion of exponential growth with respect to periods of linear time (represented by the dimensional power of e).

However, though not immediately intuitively obvious, we could equally consider the notion of exponential growth with respect to a cyclical (or circular) notion of time.

You might easily recall that the circumference of a circle is given as 2 * pi * r (where r is the radius).

Therefore in the unit circle (where the radius = 1) the circumference = 2 * pi.

However in the complex plane, imaginary as well as real measurements of the radius are involved. So using the imaginary scale, the circumference of the unit circle = 2i * pi.

We have moved here in fact from a linear to a purely circular notion of dimension.

Common intuition would suggest that as every number raised to the power of 0 = 1, that this must also be the case with respect to e!

This would then suggest that the circular circumference 2i * pi somehow must imply 0.

This is where it gets very interesting, as in fact ultimately we have to consider two distinct notions of 0 (which cannot be properly clarified within the merely quantitative parameters of conventional mathematics).

The imaginary interpretation of the circle implicitly entails a more interactive notion of meaning where opposite directions of the radius (positive and negative) cancel out. In dynamic terms, this implies attempting to fully equate both the linear notion of the line diameter with the corresponding notion of its circular circumference so that both are ultimately identical.

This can only be envisaged through the continual shrinking of the circle, so that in the limit, when it approaches the common point at its centre, both the diameter and its circumference are by definition identical. At this stage real notions of finite extension have disappeared so that we are left - literally - with an “imaginary” circle.

Having been deeply fascinated with the Euler identity for some time, I have given considerable attention to the precise significance of the dimensional exponent 2i * pi in both analytic and holistic mathematical terms.

If you were to ask me the $64,000 question to give a simple intuitive explanation as to how mathematically, e ^ (2i * pi) = 1, I would explain it in this manner.

As we have seen, e can be most simply expressed as the limit of (1 + 1/n) ^ n as n approaches infinity. Remember we are dealing here with the (reduced) analytic interpretation!

Now 2i * pi expresses the notion of the imaginary circumference (which requires that the circumference of the unit circle be identical with its line diameter). As long as we view the circle in finite terms, both line and circumference will remain distinct. So the ultimate identification of both entails the infinitesimal notion of a common central point.

This point can be represented as 1/n (where n approaches infinity).

So therefore e ^ (2i * pi) = e ^ (1/n), = {(1 + 1/n) ^ n} ^ (1/n) = (1 + 1/n) ^ 1, which of course in the limit where n approaches infinity = 1 ^ 1 (i.e. 1).

However, I would be the first to admit that there is something unsatisfactory about this analytic explanation (which requires mixing finite and infinite notions in a manner that lacks true coherence). Likewise the appreciation that the imaginary circumference of the unit circle represents a non-dimensional point does not derive directly from analytic type interpretation.

So the true reality is that the Euler identity greatly transcends analytic understanding, requiring, by contrast, a proper holistic interpretation of its symbols so as to become intuitively meaningful.

Consider briefly these two relationships:

1) e^ (2i * pi) = 1 (as given by the fundamental Euler identity).

2) e^ 0 = 1 (as corresponding with the conventional quantitative interpretation, where any number raised to the power of 0 = 1).

At first glance this would seem to imply that 2i * pi = 0. However this clearly makes no sense from the analytic quantitative perspective.

Indeed this problem can only be reconciled through recognition of the fact that they both correspond to numbers with two different interpretations.

So whereas the second explanation corresponds directly with the accepted analytic notions of quantitative behaviour, the first implies a distinctive holistic interpretation (in qualitative terms).

We have clearly arrived at the central paradox that Benjamin Pierce referred to following demonstration of his proof.

Therefore though the Euler identity can indeed be proved in an analytic manner, it leads to a central paradox where its coherent interpretation is simply meaningless from the conventional mathematical perspective.

What therefore is involved with the Euler identity is an extreme case where the attempted merely analytic interpretation of mathematical results is pushed to such an extreme that it eventually breaks down altogether as a coherent explanation. [10]

As I suggested in the final article in “The Dynamics of the Number System” the nature of number properly should be understood in a developmental context.

Thus whereas analytic notions are fully appropriate with respect to one band of the spectrum (Band 2), they become increasingly inappropriate at a higher band (e.g. Band 4). Here the specialised holistic appreciation of mathematical symbols takes place.

As I hope to demonstrate in the next article, the Euler identity requires such holistic appreciation for its proper interpretation.

In fact the need for this alternative holistic type understanding should indirectly become evident through attempting to trace out the implications of applying the cyclical model of exponential growth to our financial investment of €1.

Instead of growth in linear time we now must consider circular notions. So we trace out a full circular revolution in the complex plane before returning to our starting value.

This would suggest that heading anti-clockwise from the point 1 on the circle (see the diagram towards beginning of article), with a quarter revolution, the investment would be worth €i, then with a half revolution – €1 , with three quarters of a revolution – €i, and the finally with a full revolution back at €1.

Strange investment indeed! Clearly it makes no sense from the conventional perspective based on analytic type notions (of a linear nature).

However as we shall see, a coherent meaning of such circular behaviour can indeed be given in holistic terms (which we will return to in Part 2).

Notes

1. The general expression e ^ ix = cos x + i sin x, can be correctly referred to as a formula, equation or relationship. The more specific expression e ^ (i * pi) + 1 = 0 properly represents an identity. I then customarily use a slightly modified version of the identity, in what I refer as the fundamental Euler identity i.e. e ^ (2i * pi) = 1.

2. The Guardian, Nov 11, 1999

3. The equation holds not only for real but for complex values of x.

4. Ln is the customary notation for the natural log (based on e). When the base number is 10, log notation is used.

If ln x = y, then e ^ y = x.

So if ln (cos x + i sin x) = ix, then e ^ (ix) = cos x + i sin x.

5. Strictly expressed, a transcendental number cannot be the solution to a polynomial equation with rational coefficients.

6. If y = x ^ 2, then the differential i.e. dy/dx = 2x. So we have here - literally - the reduction of the dimensional number 2 to its base number equivalent (expressed in 1-dimensional terms).

Remarkably the psychological process of differentiation with respect to reality is similar in that it consists of reducing 2-dimensional notions in 1-dimensional terms.

Looked on another way, this entails dualistic splitting of opposite polarities (such as external and internal) in an absolute manner. Integration then entails the reverse process whereby these opposite polarities are now treated as interdependent.

7. It is interesting to note that the very symbols we use to represent the notions of one and zero (i.e. 1 and 0) are closely associated with the geometrical notions of the line and circle respectively.

8. We need to be very careful in interpretation. For example 2 can be used to represent a base number in the Type 1 system, i.e. 2 ^ 1; equally 2 can be used to represent a dimensional number in the Type 2 system, i.e. 1 ^ 2. Both of these expressions in isolation can be given a quantitative interpretation. However in dynamic relationship with each other, they are always complementary. So for example in the expression 2 ^ 3, if 2 is interpreted in quantitative terms, then - relatively - 3 is of a qualitative nature.

In experience we continually switch as between two distinct notions of number (belonging to Type 1 and Type 2 respectively). However Conventional Mathematics gives but a reduced interpretation in Type 1 terms.

This is a most fundamental problem therefore of the greatest possible importance, which as I keep stating, urgently needs to be recognised!

9. Strictly speaking, the square root of – 1 has two roots + i and – i respectively.

These are often very closely related. For example, virtual strictly represent the imaginary (rather than real) manifestation of sub-atomic particles as matter and anti-matter which quickly annihilate each other creating energy.

Likewise in the contemplative life, approaching spiritual union, the positive and negative poles with respect to short-lived (imaginary) projections are very closely associated with each other. Alternatively we could express these as virtual projections (which are a key feature of advanced contemplative development).

10. The comparison with interpretations of quantum physical reality is relevant in this context. Clearly one cannot coherently interpret such behaviour in a classical manner.

It is similar with respect to the number system in that analytic notions fail completely here as a means of interpretation.

References:

Mike Hockney: The Mathematical Universe (the God Series): The Mathematical Universe (The God Series) e-book: Kindle Edition

Andy Smith: Getting to the Point: A Review of Mike Hockney's “The Mathematical Universe”, www.integralworld.net

Elliot Benjamin: The Mathematical Universe, Science and Euler's Formula, www.integralworld.net

Paul Nahin : Dr. Euler's Fabulous Formula Cures Many Mathematical Ills, Princeton University Press, 2011