|
TRANSLATE THIS ARTICLE
Integral World: Exploring Theories of Everything
An independent forum for a critical discussion of the integral philosophy of Ken Wilber
SEE MORE ESSAYS WRITTEN BY ANDY SMITH
Small World,
Big Cosmos
The Role of Scale-free
and Other Networks
in Hierarchical Organization
Andrew P. Smith
Summary
The past century’s great reductionist advances in our understanding of different forms of existence, including atoms, molecules, cells and organisms, have led to an increased interest in
how these holons interact with one another. Much of this research has focused on networks, which can be defined as a group of holons that interact more strongly with one another than
with other holons. Several different classes of networks have been identified, including ordered, random, and scale-free. Scale-free or "small world" networks, in which there is an inverse
or Power Law relationship between the number of links a node has and the frequency of that node in the network, are the most complex and interesting. A great many aspects of human
societies can be understood in terms of scale-free networks, but they are also found in the molecular organizations within cells, and probably in complex tissues such as the brain. These
findings have several major implications for our understanding of hierarchy, including 1) the way we classify individual and social holons; 2) estimating the degree of analogy between
holons that occupy equivalent positions on different levels of existence; and 3) the way individual and social holons evolve.
Introduction
The importance of hierarchy as an organizing principle of life is now recognized by scientists, philosophers and scholars working in many different areas of investigation, including the
metabolic processes within cells (Becker and Deamer 1991; Hartwell et al. 1999), the interactions of cells and tissues (Raff 1996), the evolution of organisms (Depew and Weber 1997; Sober
and Wilson 1998; Gould 2002), the dynamics of ecosystems (Allen and Starr 1982; Odum 1983), the development of individuals (Maslow 1968; Loevinger 1977), and the evolution of
societies (Fukuyama 1998). Many theorists have proposed grand models of existence in which all of life is arranged in a nested hierarchy, or holarchy (Ouspensky 1961; Koestler 1991;
Land 1973; Young 1976; Jantsch 1980; Wilber1995; Pettersson 1996; Smith 2000). In this view, all forms of existence--from subatomic particles to human societies, and from the most
rudimentary forms of perception to the highest states of consciousness--are holons, both wholes containing other, lower holons as well as parts of still higher holons.
Holarchy has tremendous potential as a unifying principle of existence, but before this potential can be realized, holarchical relationships need to be understood in much better detail. Ken
Wilber (1995), who has proposed one of the broadest-ranging, most ambitious of holarchies, has listed twenty tenets of holons, describing some of their relationships with each other.
These tenets, however, are couched in very general terms, and provide little insight into the specific ways that holons interact with each other. Furthermore, they describe mainly the
relationships between higher and lower holons, rather than those between holons on the same level of existence.
For example, a cell is a holon, composed of other holons, molecules. One of Wilber's tenets tells us that a cell is higher than its component molecules. It has an asymmetric relationship
with these molecules, in which it is absolutely dependent for its existence on them, while the converse is not true1. It also constrains their behavior in certain ways, while the molecules, in
turn, set limits on the possibilities of a cell. A similar kind of relationship exists between an organism and its cells.2
But what about the relationships of the molecules within a cell, or of the cells within an organism, or of organisms within a society, to each other? Such horizontal, or hetarchical,
interactions are often contrasted with hierarchical or holarchical interactions, as though they were completely separate. But any hierarchy includes both kinds of relationships. Indeed, the
two kinds of relationships are so intimately associated that we could say they are two facets of the same phenomenon. As I have argued elsewhere, higher forms of life are always created
through hetarchical relationships of many lower forms (Smith 2001c); one can't exist without the other. So understanding the principles underlying hetarchical relationships is a key to
understanding the organization of holarchy.
In the past few years, hetarchical relationships have been the subject of a great deal of innovative research. Having learned many details about certain kinds of holons, such as molecules,
cells and organisms, many scientists have turned their attention to understanding how they interact. From these studies has emerged the key concept of networks. In the context of the
hierarchy, a network may be defined as a group of holons, all on the same level of existence, which interact (in certain ways if not in all ways) more strongly with each other than with any
other holons. Human societies are networks, because we interact more strongly with other members of our species than we do with other organisms or with inanimate objects. We can also
identify societies within societies, groups of people who interact more strongly with each other than with people outside the group--families, work environments and nations, for example.
Ecosystems are networks, because we can define--geographically and in other ways--a group of organisms that interact more strongly with each other than with other organisms.
Similarly, cells in the body, and molecules within cells, form networks in which their interactions are confined largely if not entirely to a finite and fairly distinct group of other cells or other
molecules.
Typically, the component holons in a network are referred to as nodes, and their interactions as links. So in a molecule, the nodes are atoms, and the links are chemical bonds. In a
metabolic network within a cell, the nodes are molecules and the links are enzymatic reactions or other processes by which these molecules interact with each other. In a tissue, the nodes
are cells, and the links are cell-cell interactions, which may involve physical contact, the release of hormones and other chemical substances, or synaptic transmission. In human societies,
the nodes are individual people, and the links are their communicative interactions.
Understood in this way, networks are in fact essentially synonomous with social holons, as I have previously defined them (Smith 2000; 2001a,b). They are a more-or-less homogeneous
group of individual holons (cells or organisms, for example) or of social holons (molecules, tissues, human organizations) which strongly interact to form a higher-order social holon. In
asserting this, I'm aware that Wilber does not define social holons in the way that I do, and that some of his followers don’t even make the distinction between individual and social
holons3. I will not reiterate here the arguments and evidence that support the view of this relationship I take.
However, as we will see later, studies of networks provide further important support for my view. That is, everything that I define as a social holon has been, or can be, viewed as a
network as these are generally understood. In contrast, individual holons can not be understood as networks in this sense, at least not of a kind that has been characterized as such. We
can say that individual holons contain networks, but are not themselves networks. So network theory provides a new and fairly precise set of principles capable of distinguishing between
individual and social holons.
In this article, I will discuss these principles, and some of their other implications for an understanding of holarchy. I will begin by describing the different kinds of networks that have
been identified, and some of their defining properties. I will then examine in more detail the characteristics of the most complex kinds of networks that have studied so far. Finally, I will
discuss some of the ways in which this work is significant to current issues of interest to Wilberites and others who recognize hierarchy as a central paradigm of existence.
Ordered networks
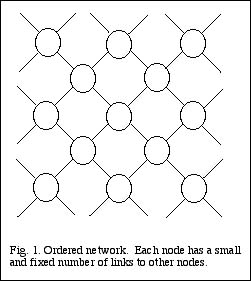
The simplest types of network are those in which each node has a relatively small and fixed number of links to other nodes. I refer to such networks as ordered. A good example is
provided by a crystal, such as diamond, composed of carbon atoms, or quartz, composed of silicon atoms. Each node, or atom, has links, or chemical bonds, with several neighboring
atoms, and only those atoms; this results in a highly regular lattice structure (Fig. 1). Any one small portion of such a network looks exactly like any other portion.
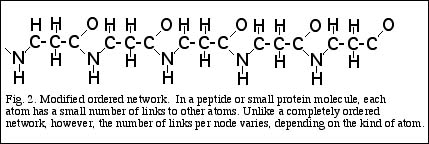
A crystal is basically a very large molecule composed of a single type of atom. But a variation on the theme of orderedness is also created when several different kinds of atoms interact to
form molecules. Consider a peptide, formed by a linear sequence of amino acids, linked end to end (Fig. 2). As with a regular crystal, each atom in the peptide is linked by chemical bonds
to a relatively small number of neighboring atoms, and these links are for the most part fixed. Unlike a crystal, however, the number of links in a typical protein molecule varies from node
to node or atom to atom, because different kinds of atoms have a different number of links. Carbon atoms usually have bonds or links to four other atoms, though they may have three, in
cases where a double bond is formed. Nitrogen has three, or two if one bond is double, oxygen two or one, and hydrogen always one. So a molecule that contains more than one kind of
atom can be regarded as a sort of modified ordered network.
So far I have only considered what might be called atomic networks, or molecules. But ordered networks are also found on higher levels of existence, characterizing the interactions
between certain kinds of cells, and certain kinds of organisms. Many relatively simple biological tissues are ordered networks. Examples would include pulmonary sacs in the lungs, acini
in the liver, and the cells of the epidermal layer in the skin and many other tissues. Within the tissue, each cell interacts with a small number of surrounding cells, through contacts of their
surface membranes. The tissue is a sort of two- or three-dimensional lattice of cells, with a fairly uniform structure throughout.
Likewise, there are very simple organisms that interact only with a relatively fixed number of neighbors. Examples include coral reefs, Hydrazoan colonies and polychaete worm colonies.
Each member of such a colony is surrounded by several other members with which it interacts. It has essentially no direct interactions with other members.
As with the example of noncrystalline molecules, we can also identify tissues and animal societies which have a modified version of the ordered structure. In this case, some holons in the
tissue or society may have more links than others, but such holons tend to belong to distinctly different classes. For example, the retina of the vertebrate eye is composed of several
different kinds of cells, including the rods and cones, which actually respond to incoming light, as well as other cells which transmit stimuli from the rods and cones, including horizontal,
bipolar, amacrine and ganglion cells. Each type of cell is linked to only some of the other types of the cells, and the number of links in each case is small and more or less fixed.
Likewise, in many vertebrate animal societies, males, females and immature members constitute classes that differ with respect to the number of social links of their members. An adult
female, for example, may interact strongly with a single male and several immature members of the society, while an adult male may interact strongly with several females, moderately with
other adult males, and weakly with some immature members. Another example is provided by colonies of social insects, where several different roles also exist, and where members
fulfilling different roles differ in the number of other members with which they interact4.
Ordered networks are not common in human societies, but some very social situations may approximate them. A rigid bureaucratic structure, such as the military, or the government of a
non-democratic country, has a somewhat ordered structure. Again, different members play different roles, but for any particular role, the number of interactions with other members may
be more or less fixed. Any very small social unit, such as a family, may also be considered an ordered network; in this case the order is pure, since every member is just as well-connected
as every other member. Ordered human social networks may also form in temporary situations, for example, when a small group of people assemble to perform some task.
Having seen a few examples of ordered networks, let's now consider some of their properties. An important question to ask about any network is its stability, that is, how resistant is it to
disruption or destruction? Network theorists commonly answer this question by testing the network's response to removal of some of its nodes. If nodes are removed randomly from an
ordered network, there is an immediate, though gradual, decline in its structure or functions. For example, if we could remove 5% of the atoms in a crystal, scattered at random throughout
the crystal, the crystal's structure would be significantly weakened. If we removed 10%, it would be somewhat more weakened, and so on. Notice, however, that there is no critical point
where removal of nodes causes the entire network to collapse. The loss of structure is gradual, and more or less proportional to the loss of nodes.
Likewise, if we could remove a few cells at random from a simple tissue, or a few organisms at random from a simple colony, we would probably observe a slight change in the structure or
function of the tissue or colony. The more nodes or members are removed, the greater the alteration, but again, there is no critical point at which the entire tissue or colony is destroyed.
This reflects the fact, to reemphasize, that each holon in such a network is more or less equivalent to every other, neither more nor less important or critical to the entire network.
In the case of a modified ordered network, such as a peptide molecule, the nodes are not equivalent. Some atoms in the molecule are much more important than others. Removal of a
carbon or oxygen atom would have more of an effect than removal of a hydrogen atom; indeed, certain hydrogen atoms are attached loosely to proteins, and come on or off according to
certain conditions. However, as with a regular ordered network, the removal of a single or a few nodes of any kind is unlikely to have a drastic effect on the function of the molecule.
The same is true of cells in tissues like the retina, and of individuals in higher animal societies. Some cells, and some members of an animal society, are more important than others, and so
their removal from the network will have a greater effect on the structure and function of the network. But again, if the network contains a large number of members, removal of a few will
have a relatively.small effect.
Another property of networks of great interest to those who study them is what is referred to as their diameter. A network's diameter is defined as the average distance, or number of links,
between any two members of the network. It's a measure of how easily any two nodes of the network can interact, or communicate, with each other. If they are directly linked to each
other, they can interact with maximum speed and effectiveness. If they are linked indirectly, with one or more other nodes between them, their interaction takes place more slowly and less
efficiently. Clearly, the smaller the diameter of the network--the fewer the average number of links between two members or nodes--the more easily these members can communicate with
each other. This in turn has important implications for how efficiently the network functions.
Consider the ordered network shown in Fig. 1. Suppose we want to move from one node to another; how many links must we travel across? If the two nodes are adjacent, only one link
separates them; on the other hand, if they are at opposite sides or ends of the network, a great many links must be traversed. For an ordered network, the average number of links
separating two nodes is thus about half the distance, or number of links, across the entire network. This is a relatively large number, and indicates that communication or interaction
between many nodes in an ordered network is relatively slow or difficult; they are separated by many links. While one node can communicate easily with its surrounding neighbors, it can
communicate with more distant nodes only through many intervening nodes. As we will see later, there are other kinds of networks where the diameter is much smaller (relative to the total
number of nodes), reflecting the fact that any node is relatively well-connected with any other node.
Random networks
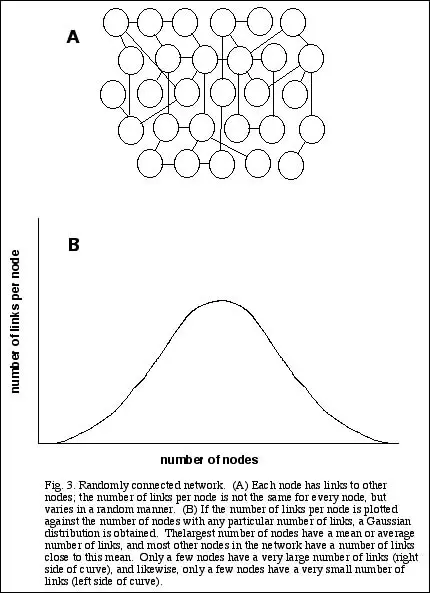
A second general class of networks is represented by those whose nodal members are connected randomly (see Fig. 3A). Rather than having a fixed number of links per node, this number
can vary somewhat. If the number is truly random, however, then there is a well-defined average number of links per node, as well as an equally well-defined coefficient of variation of this
average. So if we were to plot the number of links per node against the number of nodes, we would get a Gaussian or Poisson distribution--a symmetrical peak tailing off on either side
(Fig. 3B). Most of the nodes in the network have about the same number of links. Relatively few nodes have many fewer links than the average, or many more links.
One example of a random network is provided by the structure of proteins, very large peptide molecules found within all cells. As noted earlier, peptides are composed of smaller
molecules, amino acids, which are linked end-to-end in a chain. Very large peptides, however, do not take a linear form, but fold up into a three-dimensional conformation. In order for this
folding to occur, amino acids in one portion of the chain must interact with other amino acids situated in distant portions of the chain. So in a typical folded protein, most amino acids
come into contact with not simply their two immediately adjacent neighbors, but several other amino acids. When the number of such contacts is plotted against the number of amino
acids that have this number, a Gaussian curve results.5
Random networks are also found at higher levels of existence. An example of a random multicellular network would be a bacterial colony. Individual bacteria interact when they encounter
one another while moving about in a medium, and this is essentially a random process At a still higher level of existence, random networks characterize relatively unorganized societies of
invertebrates. An example would be colonies formed by crabs. All the members are essentially equivalent, but due to differences in such factors as size, aggressiveness, exploratory
behavior, and so on, random differences in the number of interactions per individual may occur.
Finally, we can observe random networks in some aspects of human societies. As with ordered networks at this level, most examples are likely to be found in temporarily assembled
groups. Thus participants in a seminar or workshop may form contacts with each other during the actual meeting. This kind of organization results because of certain special conditions,
including a) all members have a somewhat similar background or interest in some subject; and b) the time during which they can get to know each other is limited. As we will see in the
following section, when these conditions do not hold, as they generally do not when we consider social networks in the larger society, a different type of network usually forms.
Another example of random networks at our level of existence is found in the organization of urban areas. If we look at a road map of the U.S., or of some smaller area within the country,
we see a network in which various cities or towns are the nodes, connected by roads or highways, the links. The number of roads or highways emanating from any city is clearly not fixed,
but neither does it vary very greatly, if we consider only urban areas of comparable size. We can define an average number of highways per city, and we will find that the number of
highways linking any city will generally fall fairly close to this average.
How do random networks compare with ordered ones with regard to stability? They are very similar. If a few nodes are randomly removed from a random network, there will be some
measurable decline in structure or function of the network, but this decline will be about proportional to the number of nodes removed. As with ordered networks, there is no critical point
at which the entire structure or function of the network collapses.
On the other hand, the diameter of a random network is generally smaller than that of an ordered network. That is to say, on average, each node is connected to any other node by a
shorter chain of links and nodes. This is because a few of the nodes which have more links than average will connect with other nodes that are physically far separated from them. This
means that any nodes that are the vicinity of both ends of this shortcut will be able to contact each other through this long distance link.
Scale-free networks
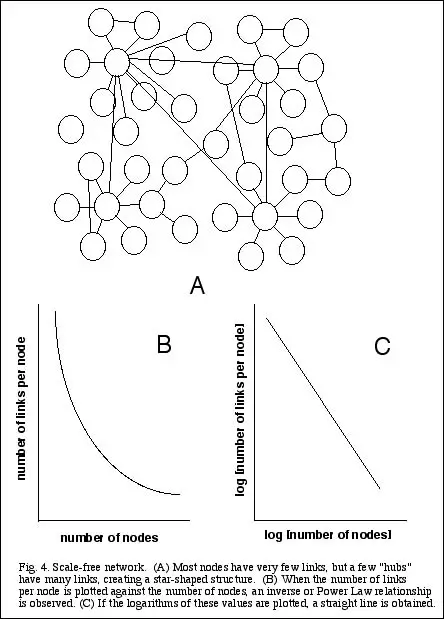
The most interesting kind of networks, and those which have received the most attention and publicity recently, are known as scale-free (Barabasi 2002; Buchanan 2002). In this type of
network, there is an inverse relationship between the number of links per node, and the number of nodes with this many links. That is, most nodes have very few links, and the more links
a node has, the more uncommon it is (see Fig. 4A). So when one plots the number of links per node against the number of nodes, one gets an exponential curve (Fig. 4B), or a straight line
on a logarithmic scale (Fig. 4C). This kind of relationship is also called a Power Law distribution, and is a characteristic feature of scale-free networks.
Scale-free networks have now been shown to exist very widely in both the natural world and in human societies. In the cell, examples include metabolic networks, in which each kind of
molecule is linked to other molecules by enzymatic reactions (Jeong et al. 2000); and protein networks, in which protein molecules are linked to each other by physical interactions (Jeong
et al. 2001; Wuchty 2001)). It seems likely that some kinds of tissues, particularly the nervous system, also exhibit scale-free organization, though so far the complexity of these tissues has
not made it possible to test this hypothesis.6
In human societies, scale-free networks include many kinds of social relationships between people, including networks of acquaintances, business contacts, and sexual partners (Barabasi
2002). It even turns out that if one "links" movie actors who have appeared in at least one film together, one also gets a scale-free network! Other examples include the scientific literature,
in which individual articles or papers are the nodes, linked to each other by citations (Bilke and Petersen 2001); and human language itself, in which words are nodes, linked by
relationships such as similar meanings or associations in speech and text (Ferrer et al. 2001). Scale-free organization has also been reported for electrical power grids. where power sources
are linked by lines to various consumer areas, and airline routes, which link cities to other cities.
The best known and most intensively studied scale-free networks, however, are the internet--the physical structure of servers and individual computers linked by phone lines all over the
globe--and the world wide web, the documents or pages of information accessible through the internet. Because of the enormous number of nodes and links involved, particularly in the
world wide web, and because this information can be accessed in a straightforward and systematic manner, a seemingly unending amount of data on the internet's organization has
accumulated, and has been subjected to rigorous statistical analysis. Much of what is known about scale-free organization has come from this work.
What are some of the distinguishing features of scale-free networks? As I pointed out earlier, this class of networks is characterized by a few relatively highly linked or well-connected
nodes, and a great many others with few links. One important implication of this organization is that such networks are highly resistant to random perturbations. Elimination of a few
randomly chosen nodes will usually have little effect on the overall structure and function of the network, because the probability is that these nodes will have few links, and not be
critical to the overall organization. This aspect of scale-free networks is thought to account for the fact that the internet and the world wide web as a whole have proven quite resistant to
random breakdowns. That is, when individual servers go down, the problem is generally confined to a small region of the web or the internet. The same property may contribute to the
resistance of cells to chemical or biological insults, or to mutations; a loss or deficiency of one type of molecule in the metabolic network is unlikely to have serious repercussions for the
rest of the network.
On the other hand, scale-free organization turns out to be much more vulnerable than a random or ordered network to a selected perturbation. If one or more of the highly connected
nodes--commonly called a hub--is eliminated or compromised, this will have potentially enormous repercussions on the entire network, because so many other nodes depend on these
hubs for their connection to everyone else. Alberto-Laslo Barabasi, one of the leading investigators of scale-free networks, has suggested that the Asian financial crisis in 1997, which
was triggered by a relatively common failure of a bank to meet certain debts, might have reflected weakening of a critical hub in the financial network. The same principle underlies the
potential vulnerability of sources of information, energy or wealth in America to a terrorist attack. And again, if we consider scale-free networks within cells, a biological agent--such as a
virus or bacterium--that is adapted to disrupting a key node within the network may have a lethal effect on the cell.
Another signal feature of scale-free networks is that they have relatively small diameters, that is, average distances between nodes. This discovery was actually presaged three decades
ago, long before the appreciation of scale-free properties, by the psychologist Stanley Milgram. Milgram claimed that virtually every person in America was no more than six links
removed from every other person (Milgram 1967). That is to say, if we select any person at random, he or she knows people who know other people who know others, and so on, who will
lead, in no more than six steps, to any other person. This has become famous as "six degrees of separation". While the number may not be as small as six, it is a very small number, and is
now believed to apply not just to people in America, but to everyone on the planet.
With more than six billion people on earth, many of them living in areas remote from the rest of civilization, this claim may seem preposterous. The key, however, is again found in the
well-connected nodes or hubs. Most people are fairly closely linked to one of these hubs; that is, they know a very well-connected person, or know someone who does, or know someone
who knows someone who does. One of this well-connected individual's acquaintances, in turn, will know someone who knows someone who knows...and quickly to any other person. In
other words, the few highly linked nodes, well-connected individuals, act as bridges that facilitate contacts between less connected individuals. Because of this property, scale-free
networks are also often referred to as small world networks. No node in such a network is very far removed from any other node7.
Hierarchical properties of scale-Free networks: differentiation, integration, complexity
The preceding discussion has provided a very brief and general description of several kinds of networks, and a few properties that characterize them. While all three of these classes of
networks are well represented in the natural world, scale-free networks appear to play the greatest role in the development and evolution of life. We have seen that cells are critically
dependent on a network of metabolic processes that has the typical characteristics of scale-free organization. The nervous system, though not yet shown to be scale-free in its
organization, certainly is neither an ordered nor randomly connected network. And a great many aspects of human societies also exhibit scale-free organization.
In fact, Barabasi has argued that scale-free organization is a natural consequence of a hierarchical organization, in which holons (a term he does not use but which very obviously applies)
associate to form higher order holons (Ravasz and Barabasi 2003). Ordered networks have little hierarchical organization, but are essentially heaps, as I define them (Smith 2001a).
Randomly-connected networks have slightly more hierarchical organization, but are still relatively simple. The most complex and developed hierarchies are clearly scale-free in their
organization, or at least belong to some class that is considerably more complex than an ordered or random network. So let’s consider these networks in a little more detail.
Every holon is by definition both a whole and a part. It is a somewhat independent form of existence, but also a component of a higher-order holon. As applied to a network, this dual
nature is reflected in two fundamental properties, which network theorists often refer to as differentiation and integration. Every node in a network is differentiated to a certain exent from
the other nodes, and to the extent that it is, it is an independent whole. At the same time, however, the nodes are also integrated, or connected, with each other, and this is what makes
them part of a larger holon. In the Wilber model, these two properties are commonly referred to as agency and communion.
Every stable, functional network or holon achieves some kind of balance between these properties or tendencies. If the nodes in a network were totally agentic or differentiated, they
would not interact to form the network. This situation is approximated by very weakly interacting holons such as molecules in a gas, or asocial organisms. On the other hand, if the nodes
were completely communal or integrated, they would lose their distinctions as nodes, and the network would become an amorphous mass. This extreme is approximated by a highly
ordered network such as a crystal, and simple invertebrate colonies like coral reefs.
Gerald Edelman and Giulio Tononi, whose research on networks concentrates on the organization of the human brain, have recently developed mathematical definitions of both these
properties, and claim that using these definitions, both properties can be measured precisely for any system or network for which we have sufficient information (Edelman and Tononi
2000). I will not present their equations here, but will simply describe the general approach taken. Differentiation is defined in terms of the number of different states that a network can
take, while integration is a measure of the degree to which the states of some nodes or holons within this network are determined by other holons.
Let's examine these properties more closely, using the brain as an example. The brain is a network composed of a very large number of neurons. Each of these neurons is connected to
other, often a great many other, neurons through synapses. At any given moment, a particular neuron may be active, that is, in the process of sending signals to other neurons; or it may
be quiescent. We will assume, for the sake of simplicity, that each neuron can adopt only these two states. At a particular point in time, then, the brain as a whole is composed of a pattern
of activity, formed by some unique combination of active and inactive neurons. Each different pattern or combination is a distinct state of the entire system.
How many such patterns or states are there? In an extreme case, in which the activity of every neuron is completely independent of the activity of every other neuron, the number of
different states would be maximal. Since we have assumed that each neuron can adopt only two different states, the total number of states possible would be 2N, where N is the total
number of neurons in the brain. This astronomically large number (N alone is in the billions) represents every possible combination of active and inactive neurons.
In reality, however, the neurons in the brain are not completely independent of each other. The activity of any one neuron affects the activity of other neurons. When a neuron is active
and sends out a signal to other neurons, this signal may alter their activity. Thus the activity of each neuron in the brain is to some extent dependent on the activity of other neurons.
Because of this dependence, the total number of states or patterns of activity that the brain can take is considerably less than 2N. Some of the states that would be theoretically possible if
each neuron's activity were completely independent of every other neuron's activity are not realizable in actuality. Some neurons are active only when certain other neurons are active--a
condition that neurophysiologists refer to synchronization--limiting the total number of possible states of the network.
The degree to which the total number of states of a network is limited by such interactions between nodes or component holons of the network is a measure of the network's integration.
The greater the degree of limitation of states, the greater the degree of integration. In the extreme case of maximum integration, we can imagine a situation in which the activity of every
neuron is perfectly correlated with that of every other neuron. Any particular neuron would be active only when the state of every other neuron was specified (active or inactive), and
likewise any particular neuron would be inactive when the state of every other neuron was equally specified in the opposite manner. Thus the system would exist in only two states. As
with the example of complete independence, however, this is an extreme case only meant to make a point. In reality, the activity of every neuron in the brain is not correlated with, or
dependent upon, the activity of every other neuron. The activity of every neuron is completely independent of the activity of many, in fact, most other neurons.
Edelman and Tononi (2000) go on to argue that the enormous complexity of the brain depends upon such a balance or interplay between differentiation and integration. They reason that
if there were a very high degree of differentiation but a low degree of integration, the brain could take on an enormous number of unique states, but there would be no way to relate one
state to another. Each state would be unique, not only different from every other state, but equally different from every other state. If this were the case, humans and other organisms
could not generalize or classify objects, other animals and particular situations in their environment, an ability clearly crucial to our survival. Nor would we be able to remember previous
events. These and many other cognitive abilities we take for granted depend on drawing relationships between brain states, on recognizing that certain states are relatively similar to other
states–that is, more similar to some states than to other states. Thus the state that we experience when we see another animal is more closely related to the (different) state we experience
when we see another kind of animal than it is to the state when we see an inanimate object. And these states are more more different from the state of being hungry, tired, and so on. Being
able to discern such relationships depends on integration, which allows certain states to be connected to other states.
On the other hand, if the brain featured a very high degree of integration but a low degree of differentiation, then it could not adopt a sufficient number of distinct states to generate the
great variety of experience we all enjoy. As Edelman and Tononi emphasize, all of us are capable of distinguishing literally billions of different conscious states--think, for example, of just
how many different faces alone we can recognize. Such variety of experience implies that there must be an equally large variety of brain states.
Edelman and Tononi (2000) thus proceed to develop a mathematical definition of complexity that takes the interaction of these two properties--differentiation and integration--into
account. Again, I will present a brief description of their approach while sparing the reader the details. The heart of their argument is based on the definition--first proposed by Gregory
Bateson--of "a difference that makes a difference". They consider an arbitrary portion of the brain--a subset of neurons--which itself is highly differentiated, that is, can adopt many
different states. They then ask, what is the effect on this subset of changes in the state of the rest of the brain? If changes in states of the latter frequently result in changes of state of the
original subset, then there is a high degree of integration between the two portions. Their states are highly correlated with, and dependent on, each other.
Moreover, Edelman and Tononi argue, each portion in effect can recognize a change in state of the other portion, because it changes its own state in response. This ability of one portion
of the brain to recognize a change in state of another portion they refer to as mutual information. The greater the number of states one portion of the brain can recognize through
correlation with the states of the remaining portion, the higher the amount of mutual information between them.
Complexity is then defined as the sum of mutual information over every possible pair of portions of the brain. That is, every possible subset--from individual neurons to progressively
larger groups of them--is considered in relationship to its complement, that is, all the remaining neurons in the brain, and the mutual information between each possible pair is summed. As
defined, complexity requires both a high degree of differentiation--so that given portions of the brain can adopt many different states--but also a high degree of integration, so that these
states can be recognized by changes in states of another portion. It turns out that complexity is a maximum when there is both substantial integration and substantial differentiation.
The concepts of differentiation and integration also allow Edelman and Tononi to identify subsets of networks within the brain, that is, groups of neurons that interact strongly with
themselves (have a high degree of integration), but relatively weakly with other neurons (from which they are differentiated). They refer to such subsets as functional clusters, and point
out that considerable anatomical and physiological evidence supports this classification. That is, the brain is composed of numerous anatomically distinct regions, and mapping studies
show that neurons in one region are better connected with each other than with neurons in other regions). There are also smaller subsets or functional clusters that have been identified
functionally, that is, by studies demonstrating correlations in their activity patterns. These data thus offer strong support for the view that the brain contains several stages of hierarchical
organization, and Edelman and Tononi’s analysis provides the mathematical tools for defining them precisely.
Evolution of scale-free networks
We have seen that while there are several different types of networks found in nature, scale-free ones seem to play the most important roles. Certainly they dominate our level of
existence, as well as play a critical role within cells and probably organisms. This raises the question: what determines what type of organization a network develops? Why are molecules
within cells and humans in societies, on the one hand, organized in a scale-free manner, whereas atoms within molecules, and some simple types of animal societies, organized randomly or
in an ordered fashion?
Studies by Barabasi and his colleagues have found that two key factors or conditions are required in a group of interacting nodes in order for them to form a scale-free network (Barabasi
and Reka 1999). First, the group must be growing, constantly adding new members. This of course is an obvious feature of human societies, as well as of most artifacts produced by these
societies. One could not have a better example than the internet. This property is also a feature of molecular networks within cells, if we take an evolutionary perspective, and recognize
that such networks did not emerge full-blown, but rather were created through a gradual accumulation of new molecular partners. The earliest such networks, perhaps found in enclosed
structures that resembled cells in some respects, probably contained a relatively few such substances. Over time, the number increased, as new enzymatic reactions made it possible for
new metabolites to be increased. As Stuart Kauffman (1993) has shown, as the number of substances increases, so does the probability that one substance will be capable of catalyzing
the formation of another substance. Once this occurs, links between substances can be formed.
In the case of multicellular networks like the nervous system, the growth is not so much physical as functional. Neurons are of course highly communicative holons, sending messages to
each other via synaptic connections. Growth of a neural network can occur when a fixed number of cells increase the number of their synaptic partners, or when the strength of existing
synapses is increased. As with metabolic networks, the growth can quickly become exponential, because whenever a new synaptic contact is formed between two neurons, it potentially
opens up interactions not just between those two cells, but between all the other cells they were each previously connected to.
A second critical feature of scale-free organization is that new nodes must preferentially link up to other nodes that already have a high number of links; that is, the more links a node has,
the higher the probability that it will get still more. This phenomenon is often referred to as "the rich get richer", and indeed, the distribution of wealth in America and most other societies
also follows a scale-free organization (Buchanan 2001). That is, rather than there being a Gaussian distribution of wealth, with most people clustered about a mean, there is an inverse or
Power Law relationship between any degree of wealth and the number of people who have attained it (see Fig. 4).
Why should new nodes preferentially attach to existing nodes that are already highly linked? Studies of the internet reveal one obvious reason in that particular system. People who are
putting up new web pages prefer to link to highly linked pages, because this will increase their own traffic. If your site is linked to Yahoo, you will obviously get many more visitors than if
your site is linked to John Brown's family pictures. Many other human social arrangements are founded on a similar motivation. People who are popular tend to attract more friends just
because they are popular; by linking up to such individuals, we potentially link to many more individuals. In other words, we obtain, in second-hand fashion, some of this
well-connectedness for ourselves.
In the case of scale-free networks on lower levels of existence, such as metabolic pathways within cells, we presumably cannot talk about the motivations of individual nodes or molecules
to link to other nodes or molecules. There must be other factors involved. A particular protein might also receive new links preferentially because it is situated in some cellular
compartment where it has better access to other proteins. Or it could have a structure that makes association with other proteins relatively easy. A metabolite might have many links
because its structure allows it to be transformed into many other kinds of metabolites.
Once such a preferential linking is established, the protein or metabolite would become of key importance to the cell. If it were eliminated or suffered a loss of function–through a mutation
in the gene encoding it, for example–the functions of the many other proteins or metabolites that interacted with it would also be compromised. So cells would evolve which favored the
formation of this substance. Under these conditions, newly evolved substances would increase their own chances of survival by associating with this hub protein or metabolite
Notice that the critical event in this process is something that gives the protein molecule or metabolite some edge, however small, in the ongoing process of forming links with other
molecules. The same is true on other levels, including our own. Let's ask, for example, why some individual people should become well-connected in the first place. A key factor, I
contend, is that society is not homogeneous; we are not born equal at birth. We vary substantially with respect to all kinds of properties, from physical size to various kinds of
intelligence, emotional qualities, and so on. We also vary with respect to our ability, and our desire, to interact with each other. Now it's well established that physical variation is of the
Gaussian, or random type, in which there is a well-defined mean, with most people clustered near this mean. If the mean height of men, for example, is six feet, most men will be close to this
height, with an equal number of greater and lesser height. At least some kinds of intelligence--those that can be measured using standardized tests--are also clearly Gaussian in their
distribution. While we do not have very good measures of social skills, it’s a reasonable speculation that these, too, are distributed randomly, initially. That is, to whatever extent social
skills result from genetic factors, these skills probably form a Gaussian distribution.
Why, then, should we see a scale-free distribution of connectedness among people? The answer must lie in the fact that social interactions, by definition, involve more than one
individual, and are constantly changing. Let's hypothesize that every individual is born with--or develops at an early age--a certain degree of ability and desire to make social contacts
with others. This ability is determined by his genetic makeup, as well as, probably, his early life experiences. At this point, the distribution of such an ability, like other human traits, may
be purely random or Gaussian. But unlike purely physical traits, and even some forms of intelligence, social skills are not static. They change, often dramatically. The more we interact with
other people, the better at it we become. People who are at the upper end of the Gaussian distribution will tend to interact more with others than will people closer to, or below, the mean.
By virtue of these greater number of interactions, their skill and their desire for such interactions will increase, leading to still more interactions.
In other words, the basis for the scale-free organization lies in a positive feedback system (this is how the rich get richer ). People begin with relatively small differences in social skills;
these lead to greater opportunities to interact with others, leading to greater differences in social skills, and so on. In this way, a purely Gaussian distribution of qualities can become one
described by a scale-free or Power Law distribution.
We are now in a position to gain an important new insight into the development of not just scale-free networks, but of their evolutionary relationship to other kinds of networks. Scale-free
networks, to repeat, depend on some inherent heterogeneity in their member nodes. Recall the earlier discussion of ordered networks, like crystals, simple tissues, and simple colonies of
invertebrate organizations. In these networks, the membership is highly homogeneous; each individual node is identical, or virtually identical, to every other node. Thus every carbon
atom can form four chemical bonds with other atoms--no more, and no less. Likewise, the cells in simple tissues and the organisms in simple colonies can interact only with neighboring
cells or organisms that are physically adjacent to them. Such homogeneity locks these networks into their high degree of order.
Development into other kinds of networks begins with the appearance of individual differences. On the physical level, these differences are present from the very beginning, in the form of
different kinds of atoms. These can combine in different ways to form different kinds of molecules. While the structure of any one kind of molecule is still fairly ordered, different
molecules, formed by different combinations of the same kinds of atoms, may differ substantially in their interactions.
The same was probably true for cells, during their early evolution. Random mutations created cells that had a slight advantage in interacting with other cells. As they formed preferential
links, a larger holon with survival advantages emerged. Then the survival of individual cells depended more and more on being able to link up with the hub cells in this multicellular
network.
Further evolution of the network into a scale-free form depends on the other factor identified by Barabasi–a growing system. As noted earlier, metabolic pathways, during their evolution,
probably fulfilled this criterion. As more and more such substances accumulated, the probability increased that some such substances could catalyze the formation of others. At this
point, a true linked network was born, and it made possible the formation of still newer substances with their own catalytic properties.
Implications for hierarchical models
The study of scale-free networks is still in its infancy. While some general properties, including mathematical characterizations, of them have been elucidated, a great many questions
remain to be answered, particularly regarding the different kinds of classes they may fall into, and how they develop and change over time. Even at the present stage, however, this work
has provided important new insights into hierarchy. I will conclude by discussing several of these.
First, network theory can help us in classifying holons, not only in distinguishing individual from social holons, but also in identifying different kinds of social holons. With regard to
distinguishing individual and social holons, as I noted earlier, individual holons–such as atoms, cells and organisms–do not have a typical or pure network structure. They contain
networks, which interact with one another, but these networks are of different kinds and complexities, and their interactions cannot be understood as simply a larger network–at least not
as a network of any kind presently understood. Another way of saying this, as I have discussed before, is that that individual holons have a mixed hierarchical structure, consisting of
both nested (holarchy) and non-nested hierarchy. Social holons, in contrast, have a pure holarchical or nested form (Smith 2002).
With respect to distinguishing different kinds of social holons, we have seen that we can classify networks into at least three kinds–ordered, random and scale-free. The most complex
social holons are scale-free networks, while simpler ones may exhibit a randomly-connected organization. Ordered networks are the simplest type of social holon, so simple that they are
essentially what I call heaps–groups of interacting holons with no or very weak emergent properties.
The classification of social holons provided by network theory can provide a critical test of competing views or models of hierarchy. Many readers will know that I have a long-standing,
if monological, debate with Ken Wilber on the form that hierarchy takes. Wilber is committed to a four-quadrant model; I claim that a single axis or scale is not only simpler, but represents
reality better. A key difference between us is our classification of social holons. We agree that human (and other animal) societies are social holons, but disagree sharply on what
constitutes social holons on lower levels of existence. Wilber argues that associations of one-celled organisms, like bacterial and eukaryotic colonies, are societies on the levels below
animal societies, and further, that planets are societies of molecules, and stars are societies of atoms (Wilber 1995). I contend that the relatively weak and non-emergent characteristics of
colonies of micro-organisms, as well as of planets and stars, barely qualify them as societies. In my model, the most developed societies on these levels–the true lower-level analogs of
human societies–are to be found within organisms and cells. Within organisms, tissues and organs, particularly the brain, represent the most advanced societies of cells. Likewise, within
cells, molecules and macromolecules interact to form societies of molecules8.
What does network theory have to say about this argument? We have seen that a great deal of human social organization can be understood in terms of scale-free networks, which have
very well-defined mathematical properties. Scale-free networks are also very evident in the molecular organizations within cells. They have not yet been established in the brain, but there
is no question that the networks in the brain are not ordered or random. In contrast, none of the lower level societies that Wilber identifies exhibits scale-free organization. Colonies of
micro-organisms are most likely randomly connected networks, while the interactions of molecules in planets are mostly ordered. Mathematical descriptions of these associations clearly
are very different from those of human societies.
It therefore seems to me that the burden of proof is on Wilber to justify his classification of social holons. The fact that human societies, multimolecular holons within cells, and most
likely multicellular networks within organisms all exhibit the same kind of organization I take as very strong support for my classification of social holons. Moreover, as I have discussed
elsewhere, this classification is critical to the one-scale model. This is because in that model, social holons exist within individual holons, always finding their greatest development in the
latter.9 So rather than view social and individual holons on different developmental lines, they form a single evolutionary /developmental sequence. 10
A second major implication of network research is that it may help us understand organization on lower levels of existence better. As I have argued elsewhere (Smith 2000), if life at
different hierarchical levels is analogous, we can learn much about holons at one level by understanding equivalent holons at another level. Currently, the most information we have about
scale-free networks comes from studies of the internet. This is because the internet provides an enormous amount of data, all of it easily accessible. This principles that are elucidated
from this work may then be used to illuminate the processes of scale-free networks on lower levels, like the brain and metabolic networks within cells. Indeed, network theory promises to
provide the strongest test yet devised of how analogous holons on different levels of existence actually are.
Finally, network theory can also shed new light on the development of hierarchy. As we saw earlier, some of the conditions favoring formation of scale-free networks have been
elucidated. These principles help us understand how complex, higher-order holons are formed from associations of lower holons. This is a major evolutionary process that, in my model,
result in development within a single level of existence. In addition, however, studies of networks may also help us understand how the transformation from social to individual
occurs–how associations of molecules become cells, how associations of cells become organisms, and how societies of humans may create a still higher level individual holon.
As we saw earlier, formation of scale-free networks is a positive feedback process, in which nodes with a greater than average number of links have a greater than advantage chance of
obtaining still more links. Positive feedback systems, however, as every engineer knows, don't go on forever, because they eventually lead to unsupportable growth and instability. In
fact, there is evidence that scale-free networks do not grow in this fashion indefinitely. I mentioned earlier that airline routes form a scale-free network. A relatively small number of cities
have become hubs, and are much better connected by airline routes to other cities than are most other cities. However, in recent years this structure has begun to break down, because
the hub cities have become overwhelmed with all the traffic. The network has begun to reorganize in such a way as to relieve this congestion, by reducing the number of links to the hub
cities, and adding more links to less-connected cities.
It may be that a somewhat analogous process has occurred on lower levels of existence, bringing to a halt, for example, the growth of metabolic networks, or of networks of cells. At this
point, the system may reorganize to form the characteristic mixed hierarchical structure of an individual holon. Further studies of networks may illuminate this process further, and in
particular provide some insight into the possible current development of a transcending new holon that encompasses all life on earth.
Footnotes
1. Actually, this is not so. Most of the molecules found within cells do not and cannot exist outside of them, except in the artificial conditions of the laboratory. The asymmetric
relationship is between the cell and its atoms. To demonstrate that a cell is higher than its molecules, another criterion must be used, or the asymmetry criterion must be modified (see
Smith 2002).
2. The relationship between organism and cell is genuinely asymmetric, and thus like the relationship between cell and atom, rather than that between cell and molecule.
3. Edwards (2002) has argued that the distinction between individual and social holons is meaningless, since all holons are composed of other holons and thus have a social nature. He
seems to accept some distinction, however. In his most recent work, he says, "I treat the collective holon as a unitary holon and not as a collection of individuals." (Edwards 2003). I have
no problem with this statement, simply adding that the unity of a collective holon is not quite the same as that of an individual holon. In any case, the important point is that Edwards
does make enough of a distinction between individual and social holons to perform separate analyses on them.
4. These examples are probably not completely ordered networks, but have some element of randomness in them (see following section). It should probably be noted that networks do not
have to fall clearly into any single group, but may have some characteristics of more than one group. See footnote 6, for example.
5. This conclusion is based on my own analysis of several protein structures. The data are available at: Analysis of Interatomic Contacts of Structural Units in PDB entry,
http://bssv01.lancs.ac.uk/StuWork/BIOS316/Bios31699/hemopexin/hemopexin4.htm.
6. The only nervous system for which the circuitry, or cell-cell connections, is known completely is that of the nematode worm C. elegans. It consists of about 300 neurons. My own
analysis of these data (available at: The Mind of a Worm, www.wormatlas.org ) has revealed that it has a hybrid type of organization. For most cells, the number of links, or synaptic
connections with other cells, falls on a Gaussian curve, typical of a random organization. However, a few neurons have a much higher number of links than the mean, the signal feature of
scale-free organization. It's possible that this hybrid form reflects the early evolutionary position of the nematode, and that more complex nervous systems exhibit typical scale-free
organization.
7. Though this statement is correct for pure scale-free networks, more recent analysis of the internet has revealed its organization is not pure in this sense (Barabasi 2001). It seems to
consist of several major domains. One of these is scale-free, but the others exist as relatively isolated islands. The existence of these islands accounts for the observation that most search
engines cannot easily find all webpages containing terms relevant to the search. They are located in areas very remote in terms of their linkage to the main domain.
8. In my original model, I considered individual molecules as societies of atoms (Smith 2000). I still maintain this view, but clearly the most complex social holons found within cells are
formed by networks of such molecules.
9. In the case of human societies, I have hypothesized that a transcending individual holon, comprising all life on earth, is in the process of emerging (Smith 2000). Because it has not fully
emerged, human societies are not expected to be as analogous to social holons found within cells and organisms as they would be following further development.
10. Wilber and his supporters are likely to protest here that the individual vs. social distinction refers to different features or aspects of these holons, not to different kinds of holons. The
fact is, though, that Wilber has used the distinction in both senses, thus conflating the meaning (see my detailed discussion of this in Smith 2001c). He sometimes refers to individual vs.
social holons, as when he contrasts individual people and their societies, and sometimes to individual (or agentic) and social (communal) aspects of holons. There clearly is not room for
both concepts in his four-quadrant model. Other writers have also noticed that there is a problem in the individual vs. social distinction (Goddard 2000; Edwards 2003).
References
Allen, T. F. H. and T. B. Starr (1982) Hierarchy: Perspectives for Ecological Complexity (Chicago: University of Chicago Press)
Barabasi, A.-L. (2002) Linked (NY: Perseus)
Barabasi, A.-L. and Reka, A. (1999) Emergence of scaling in random networks. Science 286, 509-512.
Becker, W. M. and D. W. Deamer (1991) The World of the Cell (Reading, MA: Benjamin/Cummings)
Bilke, S. and Peterson, C. (2001) Topological properties of citation and metabolic networks. Phys Rev E Stat Nonlin Soft Matter Phys 64, 036106
Buchanan, M. (2002) Nexus (NY: Norton)
Depew, D. J. and B. H. Weber (1997) Darwinism Evolving (Boston, MA: MIT Press)
Edelman, G.M. and Tononi, G. (2000) A Universe of Consciousness (NY: Basic)
Edwards, M. (2002) Through AQAL Eyes. Part 1. A Critique of the Wilber-Kofman Model of Holonic Categories. http://www.integralworld.net/edwards6.html
Edwards, M. (2003) Through AQAL Eyes. Part 3. Applied Integral Holonics: The Example of Developmental Health and Pathology in Personal and Social Holons.
http://www.integralworld.net/edwards7.html
Ferrer, I., Cancho, R. and Sole, R.V. (2001) The small world of human language. Proc R Soc Lond B Biol Sci 268, 2261-5
Fukuyama, F. (1999). The Great Disruption (New York: Simon & Schuster)
Goddard, G. (2000) Holonic Logic and the Dialectics of Consciousness http://www.integralworld.net/goddard2.html
Gould, S.J. (2002) The Structure of Evolutionary Theory (Cambridge, MA: Harvard University Press)
Hartwell LH, Hopfield JJ, Leibler S, Murray AW. (1999) From molecular to modular cell biology. Nature. 402,C47-52.
Jantsch, E. (1980) The Self-Organizing Universe (New York: Pergamon)
Jeong, H,, Tombor, B,, Albert, R,. Oltvai, Z.N. and Barabasi, A.L.(2000) The large-scale organization of metabolic networks. Nature 407, 651-4
Jeong, H., Mason, S.P., Barabasi, A.-L. and Oltvai, Z.N. (2001) Biological connections: lethality and centrality in protein networks. Nature 411, 41-42
Kauffman, S. (1993) The Origins of Order (New York: Oxford University Press)
Koestler, A. L. (1991) Holons and Hierarchical Theory. in From Gaia to Selfish Genes. (C. Barlow, ed.) Boston, MA: MIT Press, pp. 67-91
Land, G. (1973) Grow or Die (New York: Random House)
Loevinger, J. (1977) Ego Development. San Francisco: Jossey-Bass.
Maslow, A. (1968) Toward a Psychology of Being (New York: van Nostrand Reinhold)
Milgram, S. (1967) The Small World Problem. Psychology Today 1, 61
Odum, E. P. (1983) Basic Ecology (Philadelphia: Saunders College Publishing)
Ouspensky, P. D. (1961) In Search of the Miraculous. New York: Harcourt Brace Jovanovich.
Pettersson, M. (1996) Complexity and Evolution (Cambridge: Cambridge University Press)
Raff, R. A. (1996) The Shape of Life (Chicago, University of Chicago Press)
Ravasz, E. and Barabasi, A.-L. (2003) Hierarchical organization in complex networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67, 026112
Smith, A.P. (2000) Worlds within Worlds (www.geocities.com/andybalik/.introduction.html)
Smith, A.P. (2001a) The Spectrum of Holons. www.geocities.com/andybalik/.Kofman.html
Smith, A.P. (2001b) All Four One and One For All. www.geocities.com/andybalik/.allfour.html
Smith, A.P. (2001c) Who’s Conscious? www.geocities.com/andybalik/.WC.html
Smith, A.P. (2002) God is not in the Quad . www.geocities.com/andybalik/.GNQ.html
Sober, E. and D. S. Wilson (1998) Unto Others. The Evolution and Psychology of Unselfishness (Boston: MA: Harvard University Press)
Wilber, K. (1995) Sex, Ecology, Sprituality (Boston: Shambhala)
Wuchty, S. (2001) Scale-free behavior in protein domain networks. Mol Biol Evol 18, 1694-702
Young, A. M. (1976) The Reflexive Universe (New York: Delacorte)
|
 Andrew P. Smith, who has a background in molecular biology, neuroscience and pharmacology, is author of e-books Worlds within Worlds and the novel Noosphere II, which are both available online. He has recently self-published "The Dimensions of Experience: A Natural History of Consciousness" (Xlibris, 2008).
Andrew P. Smith, who has a background in molecular biology, neuroscience and pharmacology, is author of e-books Worlds within Worlds and the novel Noosphere II, which are both available online. He has recently self-published "The Dimensions of Experience: A Natural History of Consciousness" (Xlibris, 2008). 


