• home
• about
• new
• essays
• AI
• book

Joel Morrison began his life, passion, and vocation as an artist, working along the way as a multimedia designer for both Integral Institute (directly with Ken Wilber) and Integral Life. In this process of, as he would say, "waking up while building his eye," his art became ever more contemplative, culminating with his two recently self-published and lavishly illustrated books, SpinbitZ Volume I: Interface-Philosophy, Mathematics and Nondual Rational-Empiricism and Sorce Theory: Unlocking the Basement. As the original catalyst, however, his visual art maintained a critical, meta-philosophical role throughout this work, in the form of what he calls "vision-logic interfaces," catalyzing integration and elucidation in the aperspectival and nonlinear space that only the visual medium can provide. His home page can be found at www.spinbitz.net.

This essay adapted from an excerpt of SpinbitZ Volume I: Interface-Philosophy, Mathematics and Nondual Rational-Empiricism.

Post-Post-ism-ism

Kant, Wilber, Nondual Rational-Empiricism,
and the Ontic-Shadow of Post-Modernity

Joel D. Morrison

Post-Post-ism-ism: Condition-Critical in the Ontic-Shadow of Post-Kantian Dualism

Post-post-ism-ism is a “critical” condition running rampant through the body of post-post-modern Philosophy. It’s Kant’s fault … or the fault-line of those who interpreted and transformed his critical philosophy into a respectable profession fit for the LCD[1] of exoteric academia. Kant, like Descartes, set himself the task of reconciling science and religion, and protecting each from the other—“Am I going to have to separate you two?” And like Descartes, Kant’s procedure was a radical division, a dich-otomy between two zones of the Philosophical body. Both Kant and Descartes had the best of intentions, but you know what they say about the road to Hell…

Descartes’ project merely ended up in an inside-out bicameral fissurotomy[2] between the mind and the brain. No problem, we’ve just about recovered … finding little tricks to get the two halves to (feebly) interact again. Kant, however, accidentally ended up nearly severing the Philosophical body from its head.[3] Beyond the poetry of this metaphor, we will come to find that the very core of the epistemic emerges at the crossroads of these actually orthogonal dualities—cultivated into their respective polarities and triune-interfaces.

The head of Philosophy, in this metaphor, is representation—the epistemic, the real illusion—while the body of Philosophy is sub-representation—the ontic, the real beneath, or prior to the illusion. After Kant’s “radical ontotomy,” the patient of Philosophy will never be the same. But it was this decapitating fault-line that allowed post-Kantian Philosophy—now fully separate from the troublesome and unpredictable anima-mundi of the Body—into the gleaming, predictable halls of academic Science. There have been many brash young surgeons who have attempted the reconstruction, but this condition-critical has now been passed off as normal, the patient assumed healed and happy. It is now considered dangerous to Philosophy to attempt a re-connection between the dark sub-representational Body and the bright clarity of its representational Head.

The problem, we will explore near the end of this book, is that the ontic was early on con-fused with The Absolute. Kant split the ontic and epistemic into the illusory phenomena and the untouchable noumena. And hence forth, making an ontic claim was equated with making claims about the ineffable Absolute, or making absolute (dogmatic) claims in general—a waste of time and a serious symptom of dementia.

The solution to this aspect of the post-Kantian mishap, we will find, is simple, once the Vedantic doctrine of the Two Truths is allowed as a distinction between the relative and absolute scopes—allowing the ontic to regain its healthy esoteric capacity as the real and relative world of sub-representational form it always was (Brahma), and the epistemic to be the real illusion (Maya) it still wants to be.[4] It was this holarchy between relative-reality and real-illusion that Kant’s radical ontotomy, perhaps accidentally, rendered asunder. And ontology and its rational and transrational truths have been languishing in the obscurity this post-modern, ontic-shadow ever since.[5]

Another problem with the post-Kantian aftermath is that it is generally considered that Kant drew the line at the bounds of experience, beyond which metaphysics and ontology could not rationally go. This is not the case at all. Indeed, Kant—one of the most hyper-Rational (borderline pathological) of philosophers—was himself doing ontology and metaphysics far beyond the limits of experience. In fact it is generally known that Kant’s absolute categories of the understanding themselves seem to have been derived arbitrarily with little logical justification, and as a function of his language. Indeed, it is also well-known that Kant, newly “awakened” from his “dogmatic slumbers,” was roused to rescue metaphysical certainty itself from the universal acid of Hume’s radical skepticism which reduced everything to the mere coincidences of appearances. As the historian Will Durant says, the “Critique [of Pure Reason] is not precisely a criticism, but a critical analysis. Kant is not attacking ‘pure reason,’ except at the end to show its limitations. Rather he hopes to show its possibility and to exalt it above the impure knowledge that comes to us through the distorting channels of sense.”

Where experience could not go, Kant echoed the Rationalists, we must resort to logic and reason. Indeed, Kant used reason to explore the very limits of reason itself. Through logic and rationality he plumbed the very nature—the reality beneath the experience—of the thinking and knowing, rational mind. He was exploring the ontology of rationality or “pure reason,” and what he found was knowledge prior to experience, i.e. innate knowledge in the form of what he considered absolute categories, actually a metaphysics upon which to firmly ground the relative certainties of science.

The forms or categories of reason (logic and sensibility or intuition) were, for Kant, transcendental or a priori, meaning they exist and find their justification for existence before or prior to experience (this is more precisely immanent rather than transcendent, as we will see, however). Experience itself, Kant argued, cannot exist without these ontic categories of the epistemic.

As is commonly acknowledged even in academia, Kant was turning metaphysics into a science. For Kant, Metaphysics in the bad or unscientific sense, was reasoning or simple belief beyond the means or categories of understanding, not beyond experience itself. This bad metaphysics is dogma, not rationality and surely not ontology, given that Kant himself deduced his own fundamental categories ontologically and as ontic forms at the very nature of the knower himself. (To be sure, it is only because the ontic and epistemic form a polarity and indeed a holarchy that to practice fundamental epistemology—e.g. seeking the nature of the knower—is to practice a form of ontology.)

The Gyth of the Miven

As we will also demonstrate, Kant was chasing a chicken-and-egg problem, and he had to draw the line somewhere relevant to the human dilemma he was facing. Experience and reason cannot be reduced one to the other, however, not even to Kant’s “fundamental” (and arbitrary) categorical eggs of reason. There is no ultimate a priori line to be drawn (nor immaculate eggs to be found) in the ontic sand of the nature of pure reason.

As Matthew Stewart writes in his comically serious The Truth About Everything [[my comments]]:

Two related stories about Kant are important to most histories of Philosophy. The first is that Kant marks a radical turning point in the history of metaphysics. The philosophers before Kant, so the story goes, were concerned to develop metaphysical systems, and Kant demonstrated that such systems would never work. The second, more specific story is that Kant proved that knowledge is conditioned by the nature of the knowing subject, or something of the sort. Kant himself told this story. Borrowing an expression from Hume, he proudly announces his own “Copernican Revolution” in philosophy. Prior to Kant, humankind had apparently been under the impression that knowledge must conform to the nature of the object [[the “myth of the given”]]. Just as Copernicus had shown that the earth revolved about the sun, and not the reverse, so Kant supposedly proved that the object of knowledge must conform to the subject’s faculties of knowledge, and not the reverse.

… These stories about Kant are myths. The Kantian philosophy is not a real turning point in the history of philosophy. It is a continuation of the project of which the metaphysics he criticizes is merely one possible expression. … Most of his philosophy can be understood as a reenactment of what I have grandly called the dialectic of empiricism, which is itself an instance of the search for the Holy Grail of Philosophy. To be sure, Kant had a huge influence on subsequent philosophers, especially on the breed who would become the professionals of the modern university. But this just means that his name is useful as a collection point for a host of beliefs and reconstructions, mostly based on misunderstandings.

This may indeed be somewhat of an exaggeration, but there are certain truths in this account as well. Indeed, we will find Kant’s dichotomy between the Rationalists and Empiricists entirely ill-fitting, when it comes to Spinoza, and thus all the arguments against Spinoza via his status as “Rationalist” will be found suspect as well.

The limits Kant imposed on experience were themselves purely anthropocentric, and in this sense decidedly anti-Copernican. Copernicus removed Man and his earth from the center of the Cosmos, whereas Kant placed Man and his faculties back into the center of Philosophy, where he had been with the sophists before him, for example. Kant’s exemplar was also the Newtonian revolution, of which he was a champion. But it was the Einsteinian upheaval after him which—while simultaneously refuting his a priori absolute of Euclidean space and Newtonian physics—demonstrated that all bodies, such as the earth, are indeed the center of their own warped spaces, just as man is the center of Kant’s universe. Unlike Kant, however, Einstein showed that the objects of physics and their warped fields are One. The objects do not simply generate their fields, anymore than the fields generate their objects. They arise together. In Einstein’s universe, an object of matter is a congealed field, tied into self-stabilizing knots of energy. This is similar to the principle of complementarity in quantum physics. Particles no more can be reduced to waves than waves to particles. They co-evolve and co-create one another in the very same act. And in this same self-aggrandizing sense, after the “Einsteinian Revolution” of Interface Philosophy, subject and object (or given-myth and mythic-given), necessarily arise together, in a structural coupling or symbiogenesis, of sorts, as we’ll see.

In effect, Kant created a metaphysics of experience, with his metaphysical and ontological a priori (immanent) and “transcendental” categories of experience. This metaphysics itself is often used—post-Kan’t (sic)—to deny pre-Kan’tian metaphysics based on the assumption that these earlier systems necessarily go beyond the categories of experience and thus cannot be verifiable and scientific. Kant, however, outlined an entire set of categories based in the a priori understanding—his Transcendental Logic. These include causality, relation and even substance. Thus if a metaphysical system uses logical relation and causality then that system is verifiable by the means of logic and causality which are themselves a priori categories of experience. And, as we will see, these categories themselves are derived through a deep coupling with experience prior to the human modes of experience to which Kant had set his anthropocentric, chicken-and-egg limits. This logical or relational verifiability is in the same way that a mathematical proof cannot be verified by empirical means but only by means interior to its logical relations. Indeed, the notion of infinity itself is purely logical and thus entirely amenable to the understanding, and this understanding underlies all of Kant’s supposed antinomies. Infinity is simply boundless, in any of its forms. It is only the limited imagination that cannot fit the unlimited infinite into its domain. But the forms and details of logic are not bound by the perspectival restrictions of the imagination any more than is a mountain restrained in size by the horizon. And thus a metaphysical system is open to demonstrations and relations of the infinite so long as it unfolds its relations in a consistent and coherent manner. But then it can only “prove” its conclusions in the realm in which it is limited, namely logic and relation, as opposed to empiricism and objectivity insofar as our inter-objective experience with mathematics and logic is neglected.

Kant wanted to find out what happens when “pure reason,” beyond the limits of human experience, confronts only itself, but Kant’s own pool of experience was far more limited than ours today. Kant was unaware of the empirical facts of evolution and of the embryogenesis of the forms of the understanding far prior even to his a priori categories. In the light of this new experience with the natural world—e.g. evolutionary and cognitive science—we will find that experience and reason emerge together, symbiogenetically, or structurally coupled, in the very process of evolution. The “fundamental” categories are themselves inherited from billions of years of experience with the problem-solving intelligence (primitive rationality) of evolution. The “forms of sensibility,” we will see, are not ultimately a priori, in the anti-Copernican anthropocentric sense, but symbiogenetic with the sensations or experience of form. And one of the core elements of reason is the rational “acategorical imperative,” which, by itself, pulverizes the categories required by dogma.

Kant shattered the “myth of the given,” and handed us merely the “given of the myth,” the given of the ontic forms underlying the illusion of experience itself. His self-proclaimed “Copernican Revolution” demonstrated that the world is not simply given to the mind as it is in itself, but that the mind, as it is in itself, is given to experience and interpret the world. The mind, according to Kant, generates and imposes its own pre-given a priori structure and order (e.g. the categories of Time and Space) on the world before it can experience anything.

This is thesis and antithesis—from the mythic-given of sub-representation, to the given-myth and “benign user-illusion”[6] of the a priori forms of representation. The synthesis is naturally the interface between the two. As Hegel would say, “The laws of logic and the laws of nature are one. And logic and metaphysics merge.”[7] It is not the mind itself from whence the a priori categories arise. This is simply because the mind does not, and indeed cannot, exist by itself. The mind and the world are not ultimately other, but two forms of the same inter-expressive sub-representational “stuff,” and as Bodhidharma says, “vision arises where they meet.” They interact through deeper forms of inter-expression or causation common to both. The conscious mind does not generate these deeper forms and it does not create itself, but it is actually given by prior form. It is emergent from deeper emergents of deeper emergents, perhaps ad infinitum.

The mind then does not, of itself, create Time and Space and simply project them onto the timeless and spaceless world. But through its interface with the inseparable world of real duration and real relation—with which it is One—the categories of sensibility and the understanding are differentiated into abstraction in the very process of the formation and deepening of experience long before the human level of complexity arises. The mind can only know relation—as opposed to the absolute “thing in itself” free from relation—because there is only relation to be known—infinite relation, “pure” relation—of which knowledge is emergent or transcendent from sub-representational form.

As seen in the categories, Nature herself is given as the mind and to the mind to experience in its interface with the world, a part of itself. Or—to render it from the other side—the world gives itself experiences of itself through its interfaces with its minds. The experience of the “myth” is simply the interface between the two forms of the “given” emergents. Maya is the experience in the interface between the inner and outer Brahma. This within/without boundary is ultimately the interface of the positive infinity itself,[8] an infinite axis first broken open into operation in philosophical and mathematical rationality, as we will see. So it is only with a proper and esoteric understanding of rationality that this interface can be assimilated into a healthy trans-rationality.

The Kantian Legacy: “Rationalism” vs. “Empiricism”

Perhaps the most problematic consequence of the Kantian legacy is the divide-and-conquer pigeon-holing methodology he used against his immediate historical predecessors—especially Leibniz and Spinoza—forcing them into his procrustean bed of rationalists vs. their opponents, the empiricists. As Matthew Stewart writes in The Courtier and the Heretic.

In the histories of philosophy that dominate the trade, it was Immanuel Kant who sealed the fate of the two greatest philosophers of the seventeenth century. In his effort to tame philosophy into a discipline suitable for the modern academy, Kant trained his attention on the methods whereby philosophers purported to justify their claims to knowledge. He divided his immediate predecessors into two groups: the empiricists, who allegedly relied on sense experience to base their claims to knowledge, and the rationalists, who were said to derive their truths from pure reason. According to Kant's peculiar scheme, Leibniz and Spinoza wound up playing on the same side of history. Together with Descartes--the man Leibniz loathed and Spinoza regarded as seriously confused--they became the three rationalists. Leading the empiricist opposition was John Locke--the same whom Leibniz regarded as a wobbly crypto-Spinozist. He was joined by the Irish philosopher George Berkeley, whose view that physical objects are only ideas in the head strikes most readers as distinctly unempirical, and David Hume, whose ideas about the mind and causality look remarkably like those of Spinoza.

Hegel, who very much liked to see history move along in groups of three, strongly championed Kant's version of events; and the British, who were pleased to see a trio of their greatest philosophers of the period lined up against three continental musketeers, were more than happy to go along with the story, too. As a result, in philosophy classes to the present, where irony tends to be a scarce commodity in any case, Spinoza and the man who dedicated his life to expunging Spinoza's name from the world's memory [Leibniz], are presented as happy partners on the same side of a debate about the epistemological foundations of academic philosophy. Only very recently have scholars begun to rescue Leibniz and Spinoza from the revisionist schemes of their philosophical successors.

In the conventional histories of philosophy, Leibniz and Spinoza ultimately fall victim not to progress but to the idea of progress--an idea that first gained currency toward the end of the eighteenth century and that has since been taken up with gusto by all those who have a stake in presenting philosophy as a respectable, quasi-scientific discipline. Once we set aside suspect narratives of the history, however, it becomes clear that, far from being left behind by their modern successors, Leibniz and Spinoza remain unsurpassed today as representatives of humankind's radically divided response to the set of experiences we call modernity. Much of modern thought simply wanders in the space between the two extremes represented by the men who met in The Hague in 1676 (p309-10).

“Post-Metaphysics” and “Post Ontology”: An Acategorical Stance

Along with tacitly following Arthur Lovejoy in lumping most, if not all of pre-Kantian metaphysics with the Great Chain of Being, Ken Wilber defines ‘metaphysics,’ “in the bad sense” also as a postulation of ontological entities which cannot be empirically proven by science. Ironically, this would place much of science (and its hidden Foundational metaphysics)—such as “[insert your Ultimate Fundamental Object here] Theory,” and Cosmology—in the category of “bad metaphysics” or bad ontology. They all do indeed make fundamentally unjustifiable and unproven claims about the very nature of reality.[9]

This problem, to me, is part of a subtly imprecise, reactive and ontic-shy inherited definition of post-metaphysics, in this post-Kantian era of rampant post-post-ism-ism. There are clear and restrictive limits on empirical reality that science and logic must at least attempt to move beyond. Indeed, science does this all the time, and of necessity, as does Integral Post-Metaphysics with its logical necessity of an infinitely deep holarchy of ontically real holons.

Language, Buckminster Fuller tells us, was the first industry. It is based on the collective technology and invention of the word. Likewise all “language games” are forms of technology.[10] And as we would expect from the dialectic of progress, any technology that can be used, can also be abused. The technology of metaphysics is no exception. Metaphysics is abused, as Kant noted, in the taking of dogmatic stances, in postulating ABSOLUTELY the existence (not necessarily the existence of the absolute) of entities that cannot be proven. And more to the point, bad metaphysics is the absolute belief in these entities despite its detriment to the rationality and well-being of the user.

Post-metaphysics, and post-ontology, if it is to emulate the objectivity of science, cannot be fundamentally opposed to merely postulating ontically-real entities that cannot be proven empirically, because this is a necessary function of science and philosophy at the limits of the augmented senses—in the zone of pure-reason. Again, Kant himself identified the forms of logic and the forms of sensibility as the forms of understanding itself necessary to understanding anything. Mere hypothesis is not a belief system in itself, and if we restrict ourselves to the merely empirical, then we end up with a variant of logical positivism that no longer dares to wonder about what lies beyond the provincial pale of the augmented senses. A sad and safe little representational world would that be.

In any Integral and post-postmodern model, rationality should be transcended-and-included, not transcended-and-negated. Rationality is a tool, and as we will see, its very core contains the thread of an “acategorical imperative.” Thus—as demonstrated very clearly in the violently corrosive encounter between medieval dogma (metaphysics in the bad sense) and Spinoza’s nondual-rational philosophy—the very nature of truly rational metaphysics points directly into a post-metaphysics, and a post-ontology, beyond the dogma of the absolutized category. It is in the nature of the rational mind to leave itself open endlessly to new questions and analyses, and not to end on some given dogma. Dogma occurs when the acategorical truth of rationality breaks down into the irrationality of unwarranted and detrimental belief.

Post-metaphysics and esoteric rationality is then a post-ism ism. It is still a post-mythology, but it opposes a rationality-turned-mythology—a rationality twisted from its intrinsic acategorical stance to the ends of pre-rationality and its transcendent-biased absolutized categories and power structures. In short, post-metaphysics and esoteric rationality opposes the absolute category, and not necessarily the category of the absolute, as we will see. Esoteric rationality is the acategorical imperative of the open question. Its goal is to transcend the post-Kantian ontotomy of the Body of Philosophy in its radical attempt to divorce itself from the isms and dogmas of the careless skeptics and priests.

The categories of metaphysics, in Nondual Rationalism and Interface Philosophy—as in Integral Post-Metaphysics—can no longer be absolutized into a dogmatic stance, not even the absolutized-relative dogma of radical skepticism. Indeed, Nondual Rationalism, and especially Interface Philosophy, can take on any metaphysics whatsoever while maintaining the relative status of its truth claims. Metaphysics in Interface Philosophy, becomes a categorical or conceptual operating system or merely an application or program—a conceptual interface of relative categories. Install if you wish, and take it for a test run, but be aware that it is only an interface between you and the hardware of reality, and that you may have to perform a hard reboot if it fails.

Thus, post-metaphysics, in this sense, is not ultimately a feature of the metaphysical system itself, but a cognitive or conceptual aperspectival stance which imposes an acategorical imperative—a meta-metaphysical and meta-categorical framework—in which the absolute truth claims of any metaphysics are suspended in the relative world of justification, partly through the rational truth that all truth claims may be subject, endlessly, to further analysis. Indeed, this unbounded stance of analysis is at the very core of the synthesis of Nondual Rationalism, as we will see. It is a resonant thread to the positive infinity and secret of Rationalism. And, as we will see, the Vision-Logic Coordinate System and the Univocity Framework, form a meta-metaphysical framework within which metaphysics can find no foundational ground with which to dogmatize and ism-ize itself.

For example, while it may indeed be true that Spinoza believed in his system as ultimately True, it may also be true that in his age of rampant dogma, a deep faith in one’s own way out of dogma was essential to his emotional, intellectual and even to his physical growth and survival. It is also the case, however, and critically so, that nothing in Spinoza’s philosophy depends on any absolute belief whatsoever; as Deleuze says, even Spinoza’s ontological proofs are “not hypothetical, but genetic.”[11] Spinoza’s ontological proofs do not attempt to prove a transcendent God, as do Leibniz’s. They show how the relative concept, interfacing with the absolute, is properly, logically, consistently, rationally and non-dually generated.[12] Spinoza’s philosophy does not rely on the belief in the properties of an existing entity. It merely shows how to consistently and non-dually define it. Indeed, as we will see, Spinoza renders the truths of the nondual traditions into the logic of rationality. The positive infinity and secret of rationalism is the logical equivalent of Nagarjuna’s Emptiness, while Spinoza’s concept of real difference is the logical equivalent of dependent arising. Spinoza shows how and why the truths of nonduality are entirely compatible with the truths of rationality, and indeed how and why they are unavoidable and unassailable for any logical and rational mind.[13]

Indeed, it will be shown herein how and why the positive infinity of the rational does not give rise to antinomies, as Kant thought, but that the necessities of logic and relation demand the existence of the infinite. Regardless of whether the infinite can fit into the finite or indefinite imagination of man, it can very simply fit into his logical and rational understanding, itself informed in deep evolutionary symbiogenesis with experience, intelligence and memory. To be sure, only through affirming and incorporating the necessity, in the rational, for the infinite can the nondual synthesis between the relative and the absolute be truly accomplished. Just as only through incorporating the necessity of Emptiness in form, at some level or zone, can the nondual begin to present itself.

Spinoza demonstrated that there is a valid way to generate and conceive the nondual absolute in the crystalline rigor that the geometrical method of the Ethics helped to provide. More than he believed in his absolute knowledge of its properties, he believed in the rigor of its underlying form and nondual truths, as well in the transformative power in its theory of emotions. Spinoza was a test case of his own model, and in the history of Western philosophy there is no better example of a philosopher who lived, practiced and embodied his philosophy. His theory of the emotions, Spinoza declares, helped him to achieve “blessedness” or transcendence from the passive into the active emotions in the “intellectual love of God.”

The rational stage of development gives us the open-ended tools of logical synthesis and analysis. Any Integral and post-metaphysical system, therefore, must transcend-and-include these tools to make it successfully and fully into a healthy stage of trans-rationality. But it can only do so if the rational tools and truths themselves are properly developed. We will find, however, that the tools of rationality were buried under layers of mis-representation. They lay rusting, trampled under-foot in the dirt of obscurity. Resurrecting and expanding this tool-set is part of the project of this work, in order to properly and much more powerfully transcend-and-include the truths of the rational into the trans-rational free from the post-Kantian ontic-shadow.

Thus, we can state that part of the definition of the trans-rational and post-metaphysical must be the abstinence of making truth claims contrary to, or without regard to, the truths of the rational stage of development. And we can also state that such a system must be in accord with the available evidence and methodologies from the scientific and empirical world. Where no empirical evidence exists, then, we have only the tools of logical synthesis and analysis, along with trans-rational intuition. Those metaphysical systems, such as Dogmas, that run counter with the injunctions of the cognitive tools evolved so far are therefore “metaphysics in the bad sense.”

Aside: A Wilber Encounter of the Third Kind

After getting to know Ken Wilber—working directly with him at his Integral Institute for the past two years—I dearly love and greatly admire the man. But he is, after-all, a man. And when the exalted authority of one man stands in the way of the emergence of pragmatic and logical truths in another, less known sphere, this authority must be questioned. It is in this healthy and loving way that I attempt to inform the exoteric Received View of Spinoza in Wilber’s work with my studies in esoteric rationalism .

In a recent encounter[14] with Ken, he made the claim that Spinoza’s philosophy could not be post-metaphysical because Spinoza himself was not enlightened. But Wilber also makes the claim that Spinoza was “by his own admission a dedicated Cartesian.” Indeed, Spinoza wrote an early book on Descartes, within the confines of which he remained true to the Cartesian system, but only in order to render it and study it correctly. It is this early dedication to which Spinoza spoke, and to which Ken alluded. In Spinoza’s mature work, as noted by most Spinozists, he went radically beyond Cartesianism.

I challenged Wilber on this claim, stating that the majority of Spinozists would disagree with the assumption that Spinoza could be classified as a dedicated Cartesian. He then promptly retracted it, with the off-hand comment that it was irrelevant to his points. On the contrary, it is precisely relevant. The fact that Wilber could not defend his own claim shows that he adopted the maxim second-hand, and perhaps has lost the context. Anyone who really knows Spinoza’s philosophy—i.e. from studying him in depth, not just in passing on the way to a vast meta-theory of everything (and everyone)[15]—knows that Spinoza was profoundly anti-Cartesian. This is why the Theosophists consider that Spinoza’s philosophy, when reconciled with Leibniz’s (reactive interpretation), would reveal the “spirit of esoteric philosophy” in opposition to the philosophy of Descartes.

Again, the esoteric understanding of Spinoza is profoundly anti-, or trans-Cartesian. Indeed, as Deleuze states in Expressionism in Philosophy: Spinoza, [my emphasis] “…there is no Cartesian axiom [in Spinoza]…that does not take on a new meaning, hostile to Cartesianism, on the basis of the new theory of distinctions. The theory has as its fundamental principle the qualitative status of real distinction. Detached from all numerical distinction, real distinction is carried into the absolute, and becomes capable of expressing difference within Being, so bringing about the restructuring of other distinctions.”[16]

The Spinozan theory of distinctions, as we will see, transforms the dualistic independent arisings in Descartes, ultimately into dependent arisings. This dependent arising is one of the key elements of nondual philosophy, and it is a necessary outcome of the acategorical imperative of esoteric rationalism itself, as we will see.

Given that Ken Wilber has not found the plane of consistency in Spinoza’s philosophy—following his claims that Spinoza is a “dedicated Cartesian,” which he cannot back up—then it is clear that Wilber has not properly followed the injunctions of the Spinozan paradigm.[17] This assertion, then, that Spinoza was not enlightened, is a clear and uncharacteristic example of metaphysics in the bad sense. It is a truth claim about the nature (ontic) of Spinoza’s mind that not only cannot ultimately or absolutely be verified, but one whose relative merits Wilber himself has not attempted to validate with the relative truth claims available to him, namely reading Spinoza to the point of understanding, or even reading the main Spinozists, rather than merely his critics. In order to assert that Spinoza was not enlightened one must first understand Spinoza, and when one understands Spinoza, one sees that he was anything but a “dedicated Cartesian.” As Matthew Stewart noted, Spinoza considered Descartes to be seriously confused, as any nondualist to any dualist.

As we will see, there are many thinkers who have found enlightenment through Spinoza’s philosophy and who feel indeed that Spinoza was enlightened himself. These are thinkers who have studied Spinoza in depth, i.e. thinkers who have followed the injunctions of the Spinozan paradigm, such as Arthur Schopenhauer, the Theosophists, and many others in both eastern and western nondual systems.

Post-Metaphysics and the Transcendental Injunction

Another key to the definition of post-metaphysics, then—as given by Ken Wilber—is that any post-metaphysics must have an injunction for transformation beyond the merely cognitive sphere of concepts. Wilber states that the Spinozistic philosophy cannot be post-metaphysical because Spinoza had no injunctions for transformation, say, in the emotional or “spiritual” sphere. Now, anyone who knows Spinoza knows that the sole purpose of his philosophy was as a means to achieve blessedness in the “intellectual love of God.”

As is well known in the history of philosophy, Spinoza did not merely philosophize, but he was among the few western philosophers to have truly lived his philosophy. This is why Deleuze calls him the Christ of philosophy, and the common image of him is that of a saint. Like Aurobindo, writing was itself a practice for Spinoza. But more than this, Spinoza’s philosophy of the emotions—when lived as Spinoza implored his readers to do as well—was full of injunctions for moving philosophy into the practical sphere of emotional transformation, away from the “passive” or reactive emotions, to the higher “active” emotions such as the intellectual love of God. For Spinoza, as we will see, the emotional and the intellectual spheres were never separate. Philosophical injunctions necessarily transcended-and-included emotional ones. This is why Deleuze called Spinoza’s philosophy a “Practical Philosophy.” Philosophy, for Spinoza, was a practice for emotional, spiritual and intellectual development, none of which could ever be separated, because the intellectual love of God was itself an emotion manifesting the spiritual in the intellectual.

And further, Wilber states that maps of reality themselves can often be “psycho-active.” Indeed, as the maxim goes, “right thought leads to right action.” And it can easily be inverted, “right action leads to right thought.” The I and the IT quadrant, for both Wilber and Spinoza, are symbiogenetic. One does not exist separately from the other, and thus what you do in one sphere influences the other, and back and forth simultaneously.

It is in this way, that Philosophy itself, if lived and practiced, can be an injunction and a psycho-active map for radical transformation. And, in my own case, art as well was a very powerful means for transformation, before the explicit emergence of my philosophizing. Philosophy practiced as an art, then, is perhaps even more powerful, given that it quickly removes the philosopher into an aperspectival stance from which to better philosophize and transform—turning ever new interior subjects into the exterior objects of art and writing.

[[To get a quick feel of the power of Interface Philosophy to effect a nondual expression of Rationalism and Empiricism, and the resolution to the problems engendered in the wake of Kant and post-modernity, we will take a quick detour through the core feature of Interface Philosophy, the vision-logic coordinate system.]]

The Vision-Logic Coordinate System (VCS) SIMPLIFIED

In the various “integral” models, “vision-logic” denotes a stage in psychological development, a meta-vision whereby one can transcend the limits of singular perspective and attain an integrated understanding, simultracking and integrating many perspectives at once. As Ken Wilberstates in A Brief History of Everything, vision-logic is “the capacity for taking multiple perspectives and then integrating them to some degree. Unlike formal operational thinking, which tends to be single perspective, abstract-formal, and monological…, vision-logic is postformaland ‘integral-aperspectival’ (p191).” It is called “integral-aperspectival” because it is not rooted to one perspective, and can integrate them all into a meta-perspective. It is also called “network logic” in the sense that it can begin to make networks of perspectives; moving among them, forming comparisons, higher-level systems of inter-perspective translation, co-operation and conjunction, integrating and transcending all of them, rather than being rooted defensively and offensively within any of them. But it can also take parts of perspectives and reject others to make various, loosely-held amalgam-perspectives, or maps, if need be.

A loose analogy can be drawn from the visual arts, with the difference between the limitations of a painter vs. those of a sculptor. While the painter must represent his vision from a single perspective (or a fractured perspective if he is a cubist), the sculptor can execute his vision in three dimensions, view it from any angle he wishes and effectively work in them all simultaneously because he is operating volumetrically rather than merely on a flat plane.

Now imagine that the sculptor shrinks into his own creation and begins to inhabit its various nooks and crannies, and that eventually he settles down in one location and lives out his long life. Generations later, the sculpture as a whole is forgotten, and it is soon believed that this one viewpoint and its tiny visible landscape is the sole design. [18] A “flat-earth,” or flat-land mythos now reigns.

Vision-logic, and specifically the Vision-Logic Coordinate System (VCS), serves the function of uprooting such a provincial inhabitation, launching the inhabitants back into the meta-perspective of “outer space,” allowing the territory to again become an object of perception/conception as a whole in the mind. But more critically, the VCS imparts on its user the capacity to descend and ascend, and orbit around the model at will, to see the whole complex of systems from various vantage points in a higher-dimensional space. The VCS operationalizes the key elements of vision-logic, by making explicit the roots of conceptualization itself in symbiogenesis with perception (rationalism in dependent arising with empiricism, respectively). By operationalizing the roots of the concept-percept (rational-empirical), it thus serves the function of visualizing and coordinating conceptual relationships, and perspectival networks, free from a singular rooted perspective, and at the vision-logic, or integral-aperspectival level of cognition.

It must be pointed out again, at this point, that in harmony with the Deleuzean definition of philosophy as an essentially creative act, this system itself is purely imaginary, and indeed a synthetic and even an aesthetic creation; a toy demi-mythology; Philosophy as the art and play of the concept. This system does not claim existence for itself outside the mind or the paper. The system is not conceived as a ‘pure’ platonic form preexisting all human thought and action that must descend into impure materiality. But it does indeed map—in the general and abstract way of all maps—a deeper and vastly more complex emergent territory beyond itself; A dynamic reality of conceptual attractors, dimensions, drives and motions, pushing and pulling the mind in these abstract intuited directions which are only mapped a posteriori, and even empirically, to the artificial geometries (points, boundaries, axes and planes) and concepts of the system.[19] These basic emergent directionalities of thought can be found in virtually all philosophical systems, and in the hidden structure of mathematics itself,[20] and they are essential for the task ahead, as we will see.

The Two VL- Axes: Immanent/Transcendent and Transitive

When this, the subjective, and that, the objective, are both without their correlates, that is the very axis of Tao. And when that axis passes through the center at which all infinities converge, affirmations and denials alike blend into the infinite ONE. Hence it is said that there is nothing like using the light. 

— Alan Watts, The Wisdom of the Ridiculous

The intersection of the macro universe and the micro universe will create a gate, or a door. Lao tzu called this “the door to all wonders”. This is where yin and yang merge harmoniously. This is also called the Middle Way.  

—Henry Chang

In the embryogenesis of the concept (see SpinbitZ), the ineffable absolute breaks into the relation of cognitive operation[21] first in the polarity of the Immanent/Transcendent axis and then in the orthogonal transitive axes (this will be explained shortly). In this vision-logic meta-system, then, we have only two main “axes,” which are operationalized polarities fundamental to the operations of conception, including its most abstract or generalized form found in mathematics. Because an axis, in this sense, represents merely an operationalization of a more abstract polarity, rather than the common-sense (and transitive) notion of axis as a linear direction--and to make the distinction clear between the ‘axes’ of the VCS and all others--we’ll call them “vision-logic axes” or “VL-axes.” It is important to note that unlike the axes of the Cartesian system, the orthogonalitybetween these VL-axes is not perpendicular. The VL-axes are often, however, necessarily represented merely “on paper” as linear and perpendicular axes (such as in the main diagram of the VCS which we will encounter below), and doing so can be very beneficial, so long as their real nonlinear and non-rectilinear nature is kept in mind. So the term ‘VL-axis’ can function by operationalizing a polarity, and invoking the meta-perspectival diagram and the differentiating orthogonality (not perpendicularity) represented therein, rather than forcing the mind to conceive of each of these directional concepts as uni-directional and perpendicular linearities. Viewing them as single linear axes would collapse the system to merely elements of the transitive VL-axis, as we will see.

Following along with the discoveries of the modern mathematics of the continuum and set theory, as well as being informed of Spinoza’s triune infinite (see SpinbitZ), it is best to imagine these VL-axes as being abstracted from the absolute Infinite as mere concepts or “directional aspects” (aspect infinities[22]), rather than constructed of the finite as indefinitely expanding sequences. These VL-axes, or conceptual directionalities, are as follows, roughly and respectively:

1. The Immanent/Transcendent axis (I/T axis): the omni-directional polarity of within and without, contraction and expansion, division and multiplication. This is the conceptual axis underlying Arthur Koestler’s concept of a holon (a part-whole), which leads to the notion of an infinite holarchy, extending ever inward and outward.
2. The Transitive axis: the collection of infinite, directional (or one-dimensional), linear polarities, e.g. the familiar Cartesian axes.

In my adolescence, I had an abstract dream of a “disembodied flight” across a ticking strip of “acoustic ridges,” like a pull-string for interfacing and accelerating the gear system of a toy car. At every crossing of a ridge of the strip, I would hear and feel very distinct … TICK … and another … TICK … TICK, TICK, TICK, |||||||||||||…. As I continued my bodiless travel along this linear, acoustic and tactile axis of ticking units, the pattern soon became tedious, monotonous, overwhelming. I quickly developed a trick. I began to skip units, to expand awareness up and out, and then down and inward, at will. I began to see patterned regions on the infinite line, places to which I would jump, connecting and collecting organizations—organisms, forming and informing an emerging whole.[23]

This strange little dream, typical of the abstraction of many of my oneironautic[24] escapades, gave rise in my early philosophy to the idea of “the unit as the collapsible scale.” This concept of scales as expanding and collapsing endlessly to and from their units—“a doorway into the identity of within and without,” as I called it—was an early anticipation of the concept of the holon, the “part-whole,” which had been discovered decades earlier by Arthur Koestler, but about which I was ignorant. This simple idea—that every unit is a collapsible and expandable scale, the very environment of deeper, “collapsed” units, (or every part is a whole) and its corollary that every scale is collapsible to, or expandable from, a unit (or every whole is a part)—necessitates an “endless holarchy” of collapsible/expandable unit-scales.

When reading over my old notes, I found it fascinating that this transition from the transitive “ticker-line” to the immanent-transcendent holonic axis, or the “scalaxis,”[25] as I originally called it, was directly enacted, and indeed discovered in this simple little dream. In retrospect, it seems but a vivid play session in Zeno’s hypnotic brand of toys—which themselves break into the fundamental binary VL-axes of conceptual relation—but used as a seed for my wanderings in the conceptual space of the new biological genome. I include it here for a nice little diversion into dreamland, perhaps providing a self-similar historical echo, and a convenient segue; an intuitive bridge between the transitive and immanent-transcendent VL-axes.[26]

The immanent/transcendent or I/T axis is the axis mundi, or “world axis” of esoteric philosophy. It is the axis between the micro and the macro universe. We encounter the I/T axis and its polarity (as well as the concept of involutionand evolution, to be explored later)[27]* in the following quote from Plotinus, “there is nothing transcendent that is not also immanent,” and in this aphorism from Heraclitus, “The way up is the way down, the way down is the way up.” The I/T axis has been implicit throughout recorded history in one form or another. As Karin Verelstdemonstrates—in her article Some remarks on the relation between the microcosmical and macrocosmical instantiations of the mythological World-Axis—the axis mundi is found virtually throughout all religions and philosophies of the world. In the trinity of Western religions, Judaism, Islam and Christianity it is generally symbolized as a tree, such as the trees of life and good and evil, as well as the Kaballistic Tree of the Sephiroth. It is also found in the East, in the religions of India, China and Indochina. In Taoism, for example, it is known as “the door to all wonders,” and in ancient Mesoamerica it is symbolized in the form of a mountain, for example the Mayan sacred mountain Mixik Balamil at Zinacantan.

Take the following quote from the Corpus Hermeticumof the 3rd Century, “God is an intelligible sphere whose center is everywhere and whose circumference nowhere.”[28] And the I/T axis is found in tetrahedral or systematic-structural form in Buckminster Fuller’s idea of the “Omnidirectional Halo” which he describes thus, “The difference between nonconceptual, nonsimultaneous Universe and thinkabilityis always two tetrahedra: one as macro, to complete the convex localness outside the system, and one as micro, to complete the concave localness inside the system, to add up to finite but nonconceptual Universe.”

It must again be emphasized that despite the linear connotations of the word “axis,” and the necessary linearity of some of the vision-logic renderings (or interfaces), the I/T “axis” is not properly conceived as linear or uni-directional at all, but rather is inherently omnidirectional. The I/T axis is an axial representation of the unbounded polarity of volumetric, or geometric expansion or contraction (see Figure 6, below).

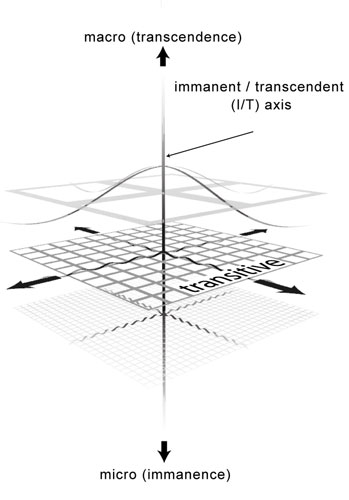Figure 6 : The Main VCS Diagram: This diagram is perhaps the simplest of the many ways to represent the distinction between the immanent and transitive axes, but it is critical to note that the diagram flattens the dimensionality of the transitive space into planes in order to represent the I/T axis uni-directionally. The omni- and non-directionality of the I/T “axis” is here drawn, unfortunately but necessarily, as a linear “axis” rather than an inherently volumetric, spherically coordinated polarity.

In the figure above, the I/T axis is drawn, unfortunately but necessarily, as a linear, unidirectional, “axis” rather than an omni-directional expansion or contraction. The transcendent “direction” on this axis zooms outward from any “position” (fixed volumetric scale) on the I/T axis and the immanent “direction” zooms inward. The familiar 3-dimensions, xyz and all infinite uni-directions in-between, have been collapsed—for the sake of higher-level, aperspectival, visualization—into the transitive plane fixed upon the central I/T axis. Also note that the orthogonality between these VL-axes is represented by perpendicularity, which is also entirely misleading. Perpendicularity is simply the easiest and most direct way to visualize orthogonality. The orthogonality between these two VL-axes, however, is best understood as a scale invariance between transitive relations. In other words, in a system of transitive relations, such as any mathematical geometry (or self-similarity), if you change the scale itself (changing coordinates on the I/T axis) the pattern of relations will always remain the same.

The crucial function of this diagram is to demonstrate the relation between transitive planes as fixed with respect to specific positions on the Immanent/Transcendent axis, and that these “positions” correlate in this higher-dimensional interface, not to position itself, but to size or scale. But it is more crucial, when needed, to be able to forget the unfortunate flatness of the transitive axes and planes, and the linearity of the immanent-transcendent axis in this rendering. We will see a more accurate rendering below of this critical distinction which, when used in conjunction, will help us recall the omni-directionality and continuity of the immanent axis, vs. the linearity of the transitive and that the transitive axis always functions from a fixed frame of reference.

The crucial point here is that the transitive axes regularly collapse (or instantaneously manifest) the immanent/transcendent infinities, as Zeno demonstrated, otherwise any distance between two points would be infinite, and the hare could never overtake the tortoise, nor the arrow reach its mark, since there are an “infinite number” of “infinitely small” intervals to cross between them.[29]

The most crucial distinction between the I/T axis and the transitive polarities is that the I/T axis deals exclusively with a priori volumetric omni-directionality, inward-and-outward, and the transitive axes are exclusively unidirectional abstractions, such as the 3 uni-directions that make up Cartesian coordinate space.

Coordinates on the Immanent-Transcendent Axis

When one dives into endlessness, in both time and space, farther and farther without stopping, one needs fixed points or milestones past which one speeds. Without these, one’s movement does not differ from standing still. There must be stars along which one shoots, beacons from which one can measure the road covered. … He must divide his universe in distances of a specific length, in compartments that repeat themselves in endless series.

— M.C. Escher, Approaches to Infinity

A quick look at coordinates on the I/T and transitive axes will help make the distinction clear. To aid in representation, we can use an enclosing surface, a sphere (see Figure 7, below), representing or embodying the particular volumetric scale. This sphere is a coordinate, on the I/T axis; a fixed scale which is inherent to (unfolding as) the particular transitive axes, represented as a plane on the main VCS diagram (above).[30] And so even the rational and continuous numberline, such as that drawn on a Cartesian graph (or any of the single lines passing through the infinity within the I/T axis below), is, in a sense, merely a uni-directional, or transitive, cross-section or rendering of the spherical/omni-directional I/T axis.

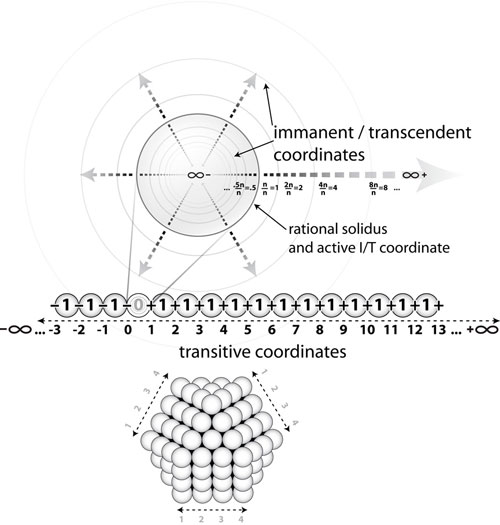Figure 7: The Nuclear VCS Diagram With Coordinates: This diagram is from Part Two: Interface Mathematics (p201) section later in this book, so some of the notation may be a bit unfamiliar, but it offers another way of visualizing the difference between the I/T and transitive axes. The I/T axis represents the infinite omni-directional aspect of scale and the transitive represents the uni-directional axes of measurable distance.

On the immanent-transcendent axis, coordinates (i.e. “positions” on the representational axis, not necessarily in space itself) denote inherently spherical or volumetric differences, as degrees of omnidirectional expansion and contraction, of the “spherical coordinate,” regardless of real-world position. In other words, the position on the immanent-transcendent axis does not represent spatial position. It represents scale, denoted by the variable size of the sphere (see above), which itself is the representation of the actual coordinate in “immanent-transcendent space.” This “immanent-transcendent space” (a space of “intensive forces,” as Deleuze might say) is merely mapped abstractly, as a visual aid, by the linearity of a transitive axis, as in the main VCS diagram (see Figure 6, two figures above, p142).

This omnidirectional expansion and contraction inherent to the immanent-transcendent axis, is opposed to the linear, unidirectional movement from position to position, number to number, on the transitive axes, where changes in position on the axes correlate, often directly, to actual changes in space.[31]

The coordinates on the transitive axes are fundamentally composed of quantized finite unities or unit-spheres, and merely abstracted as infinitely-precise positions (implicit singularities) with no volumetric extension whatsoever. This is very loosely analogous to the difference between scalars (magnitudes) and vectors (directions), except that scalars are represented as a function of abstract magnitude and the I/T axis maps the polarity of volumetric scale itself as magnitude.

I/T Omni- and Uni-axes

The immanent-transcendent axis, can be further analyzed, delineated and differentiated, into ONE omni-axis which is composed of an “infinite number” (or the numberless ALL) of uni-axes; this is the univocal ONE-ALL relation, as we will see.[32] The omni-axis is best demonstrated mathematically as a “Zenonian binary tree and semi-lattice,” as shown by Karin Verelst in her paper, Zeno’s Paradoxes. A Cardinal Problem: I. On Zenonian Plurality, and as we explore in great depth later.[33] In this paper Verelst demonstrates that this “simultaneous ‘through and through’ division”—what we are calling the omni-axis—is identical to Cantor’s uncountable infinite and the cardinality of the transrational continuum—and thus it is the conceptual incarnation of our PNDR.

The uni-axis is the I/T axis as we have already seen it in the Nuclear VCS Diagram above. The uni-axis is always centered on a single position, whose “infinitely small” Euclidean point is its unbounded immanent pole, and whose transcendent pole “reaches to” the unreachable transcendent infinity of the ONE-ALL. The uni-axis, therefore, is always conceived through the relative aspect of position or finite locality (relative to any other) and, therefore, ultimately through the “eye” or aperture (boundary or spherical “yard-stick”) of the transitive unit i.e. the spherical coordinate making up the linear directionality of the transitive-axis.[34] The I/T uni-axis is the immanent and transcendent, internal and external boundless dimension of this spherical, a priori-extended unit.[35]

Conversely, the immanent-transcendent omni-axis (or just the “omni-axis” as we will often call it) enfolds into its concept the labyrinth of the continuum of extension itself, and all of its “infinitely infinite” positions; EVERY conceivable and inconceivable, rational and trans-rational location—each one of which is the immanent pole of a uni-axis. The omni-axis, then, contains all, or omni-, of the uni-axes. This omni-axis, therefore, “is an [abstract] sphere whose center is everywhere and whose circumference is nowhere.”[36]

The omni-axis can be seen as the abstracted and generalized essence of the ancient esoteric anima-mundi (or world soul), with its ONE as ALL, whereas the uni-axis can perhaps be seen more as the axis-mundi of the I/T axis in general, with its ONE vs. its one implicit singularity and immanent pole.

I/T Interfaces, the Omni-Uni and the Omni-Non

Because the immanent pole of each uni-axis represents an “infinitely small” Euclidean point, or an implicit “singularity,”[37] it is thus the identical opposite of extension and continuity itself. It is therefore the non-extension of the abstracted immanent aspect of infinitely precise locality. This is why the labyrinth of the continuum itself exists, because the continuity aspect cannot be formed agglomeratively from its identical opposite in the Euclidean point. But, as we will see,[38] and according to the Principle of Absolute Reversal, the identical opposite of the extensionless point in the continuum is found by taking the concept to the ineffable absolute scope, and this is the polarity enfolded in the uni-axis, i.e. between the immanent point and the transcendent continuum.

The uni-axis is thus the omni-non of extension with its polarity and cultivated third between omni-extension in the ONE and the non-extension of an immanent singularity at one Euclidean point. An interesting feature, therefore, shared between the infinite I/T uni-axes, and the one omni-axis which they compose, is that they ALL converge and overlap at the transcendent pole of the ONE. At the same time, however, the immanent poles of any two selected uni-axes, at whatever scale you may choose, are separated by an “infinite number” of other uni-axial singularities (see Figure 8-A below).[39] This recognition—that two points can be “infinitely close” together and always infinitely far apart, in terms of other points—is one of those counterintuitive, labyrinthine aspects of the absolute scope of immanence (or yin) and continuity which Leibniz recognized in his exploration of the continuum. He reconciled it finally, as we will see, in his secret “Spinoza studies,” of 1667[40] when he acquired Spinoza’s (now famous) Letter XII on the infinite. At this time, Leibniz began to see mathematical points not as Euclid saw them, as elements “composing” the continuum, but the reverse, as Spinoza saw them, essentially as immanent aspects (singularities) abstracted from The Infinite univocal ONE is ALL.[41]

Identically-opposed to the immanent singular infinity of the I/T uni-axis is the infinity of singularities of the omni-axis. The omni-axis is the I/T-axis, and its Euclidean singularity, conceived not as a finite unity[42]—or “one” single uni-axis and abstracted position—but as an infinite totality of uni-axes, “composing” or a posteriori abstracted from the labyrinth of the a priori continuum of the undifferentiated absolute scope. Because the omni-axis is omni-local, it is also non-local, in the sense that it does not differentiate one uni-axial position from any other, but conceives of them all as an undifferentiated continuum of loci making up the singular ALL of extension. To take on ALL positions is to take on none of them and thus the omni of position is also its non, as we would expect with the Principle of Absolute Reversal and the univocal aspects of the absolute scope.[43]

The omni-axis is the IT axis whose locality aspect is “seen” (or unseen) at the absolute scope, through the “eye” of Infinite Unity[44] to give us omni-non-locality.[45] Poetically speaking, in the omni-axis, the pupil of the eye of locality and its boundary is fully and entirely opened, so that the eye itself—and its limiting/enabling differentiated, boundaries, positions and perspectives—has actually disappeared in the complete omni-directional opening of its boundary. This, in part, is the continuity aspect of The Infinite.

The omni-axis is the VCS representation of the ‘ONE-ALL’ tautology and identity of univocal multiplicity, whereas the uni-axis is merely the locus of the ‘one’ of “finite unity;” i.e. the immanent singularity and its boundary, respectively.[46] This distinction between the absolute unbounded ‘ONE’ and the relative ‘one’ of boundary will be explained in much more detail in the section on Unity and Nonduality. But it is important to note that both the uni and omni forms of the immanent-transcendent axis—as all VL-axes of the Vision-Logic Coordinate System—are mere abstracted aspects of “The Infinite,” as we will see in the section on Spinoza’s Triune Infinite.[47]

Recalling the two previous diagrams of the immanent-transcendent axis, we can simplify, modify and compare them, side by side, to differentiate-and-integrate the omni- and uni- axes (See Figure 8, below). The interface or cultivated third of the immanent/transcendent polarity in its omni-non-local aspect (i.e. the omni-axis), is a transitive “plane,” (see side A of Figure 8, below). Recall, however, that the image of the plane is a mere convenience, both of speech and of imagination. For the sake of higher-level, aperspectival, visualization and simplification of the omni as a uni-directional axis, the familiar 3-dimensions—xyz and all infinite uni-directions in-between—have been collapsed into the “transitive” planes fixed upon the central I/T “axis.” Such transitive planes—“planes of existence” or “levels of reality” as they are often called in cosmogonic texts[48]—in the real world correspond to the emergent/transcendent, yet relatively fixed scales (or “Kosmic grooves”) of nature, such as the “Planck scale,” the level of atoms and the level of cells. The “transitive plane,” therefore, is actually a planar cross-section of an infinite volume or extension whose vastness is defined relatively and transitively to a specified scale (coordinate on the I/T axis) of a priori volumetric spherical units. Each one of these nested (holonic) units, however, is the spherical and omni-directional I/T interface of a single uni-axis.

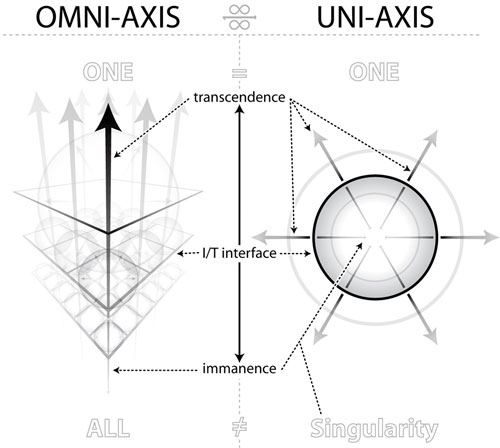Figure 8: The Omni and Uni Axes and Interfaces: Figure A shows an “expanded view” of the omni axis and the “transitive planes” as the interfaces of the immanent and transcendent directions in the omni-axis. If we collapse the representationally expanded planes, again overlapping the spheres making them concentric, however, we can see that the transcendent direction is not really upward, or linear, but outward, from all points of the continuum. Each of the boundless series of nested spheres in the transitive plane of the omni-axis is the interface of a uni-axis (B) ALL of which are contained in the omni-axis, and each of the points making up the volumetrically extended continuum of the omni-axis is the immanent pole or Euclidean singularity of a uni-axis. Note also, that as we move immanently on the omni axis, the number of uni-axes between any two (and their spherical interfaces) increases indefinitely, and—at the absolute scope of The Infinite ONE-ALL—actually is infinite.

At this point an interesting relation has begun to appear between the ALL-ONE, the omni-non and the aspects of position and extension (or continuity). The omni-non of position, recall, is the ALL-ONE, or the “omni-uni” of extension (the omni-axis), and the omni-non of extension is the omni-uni of position (a single uni-axis between the ALL-ONE and the singularity). This gives us an interesting polarity between the aspects of position and extension (or continuity) when taken at the absolute scope of the omni, or the ALL—which is the infinite multiple aspect of the ONE of Infinite Unity at which both omni and uni axes converge.[49] The aspects of extension and position, when taken at the absolute scope, appear to be identical opposite of each other, in this sense. But in quantitative terms, the uni-aspect of the uni-axis (the one singularity) is finite and the uni-aspect of the omni-axis (the ONE of ALL uni-axes) is infinite. The quantitative difference between the uni-aspects of the uni- and omni-axes (i.e. the ‘one’ and the ‘ONE,’ respectively), therefore, presents us with the critical polarity underlying the Cycle of Unity, as we will see.

While the omni- and uni- axes converge at the transcendent pole, the interfaces of each are vastly different. The interface of the uni-axis, as we have seen, is an arbitrarily defined mathematical, or real-world emergent, spherical/spheroidal boundary, whereas the interface of the omni-axis is an infinite expanse of a mathematical/metrical or physical substrate; e.g. a cubic grid or an “isotropic vector matrix” of imaginary or real metric units or a relatively uniform volumetric expanse of real atoms; a “level of reality,” or a “plane of existence.” The polarity between the I/T interfaces, therefore, swings us from the unity of the relative (finite unity) in the unit-interface of the uni-axis, to the unity of the absolute (Infinite Unity), in the ALL-ONE. This is key, as we will see, in the Cycle of Unity.

A Concluding Note on the VCS: Integrating the Differentiations

The tendency when we delineate all of this stuff and break it down into its subcomponents, with infinite levels of transitive planes exfoliating from an immanent-transcendent axis (itself composed of two types), is to forget to put it back together. The immanent-transcendent and transitive axes ultimately form an orthogonal polarity, a conceptual symbiosis. The first unit, the number 1, emerges from the uncountable I/T axis as the decided unit-boundary, the chosen scale of measurement, allowing the transitive operations of addition and subtraction (and in physical reality, agglomeration and evolution) to begin. Then, with the operations of division, the immanent-transcendent axis is again invoked or awakened as the mathematical ratio dissolves or “violates” the “closure property” and opens up the immanent pole of the Rational numbers (all of which we will discuss in detail in Interface Mathematics).

Furthermore, these infinite levels abstracted and represented on the immanent-transcendent axis, do not necessarily exist somewhere else, in the erewhon of “mere mathematics,” or in different worlds, but, as SpinbitZ: volume II will explore in depth, they emerge into every scale as the very forms of the relative, such as the “ergodic” and fractal complexities of nature (see Saturn’s rings, for instance that manifest the infinite complexity in its energy fields, as an instance-definition of ergodic).

With this conceptual framework in mind, our task ahead will be much simpler because we have made explicit the many implicit, “pre-fused” differentiations that so often conflate and “con-fuse” these absolute-level discussions, manifesting in the various paradoxes of the infinite, and of free-will vs. determinism, for example. We can now cast aside the shells so often unwittingly employed in the game of philosophy and, perhaps for the first time, begin to move these symbols around freely, on our conceptual game-board, in the light of reason.

Condition Still Critical: Waking Up from the Post-Op Nightmare of the Kantian Radical Ontotomy

In the wake of Kant’s “radical ontotomy”—nearly severing the ontic-Body of Philosophy from its epistemic Head—the task of post-Kantian philosophy must be one of reintegration of this drastic differentiation. As we have already discussed,[50] but are now better equipped to fully understand, Kant and Descartes can be seen as similar, if orthogonally opposed, figures in the History of Philosophy in its transformation into a scientific and respectable discipline fit for the gleaming halls of the academy. Like Descartes, Kant’s project was to rescue both Religion and Philosophy from the ravages of the extreme versions of the other. And like Descartes, his method was to radically “divide and conquer”—a perhaps necessary, but brutal, “ontotomy.”

Descartes’ procedure, as stated previously, traced the convoluted folds of an “inside-out bicameral fissurotomy” between Mind and Brain, severing precisely along the cogito-interface itself, between the subjective and objective halves of the epistemic—a tricky operation, to say the least, and by most accounts a dismal failure. Recall that this Cartesian division is essentially transitive, as it deals with relations between the within and the without, but relative to the fixed transitive scale of perception and conception.

Kant’s incision, on the other hand, followed the outlines of the anthropocentric level in the ontic-epistemic interface-gradient—the emergent transitive-plane of representation-level complexity or “excellence” bisecting the immanent/transcendent omni-axis with its collective landscape of human, representational cogito-interface units. The post-operative disaster caused from Kant’s unfortunate incision, recall, was due to the absence of a distinction between the absolute and relative forms of ontic knowledge and truth—e.g. the Vedantic “Two Truths doctrine.”

Kant divided the body of Philosophy into two separate worlds, the “phenomenal” and the “noumenal.” The noumenal world, according to Kant deals with things as they are “in themselves”—“das ding en sich” (sic)—absolute and free from relation with other things, including the phenomenal world. While the phenomenal world (literally “appearances”) deals with the relative properties seen in the forms of “sensibility,” logic and representation. And never the twain shall meet.

In his book Foundations: A Manual for the Beginning Student of Epistemology, academic epistemologist and Kantian, Claude L. Fox writes, “Distinct from the idea of a thing in itself is the idea of a thing in relation to other things” (p18). The example Fox gives is of the relation of a father (himself) to his son, which, he says, is a property predicated to him “not because of what I am in myself but because of a relationship I bear, to some other thing.” Kant’s “thing in itself” must then go far beneath the real relations and effects caused by the real relations a father has with his sons, such as the memories of the birth, growth, development and all the good and bad times.

Kant’s “thing in itself,” then, jumps directly from representational relation, entirely bypasses the real world of sub-representational relation and reaches into the absolute scope of infinite immanence. Das ding en sich, then is an independent arising, opposing the relative world of form in dependence on—interfacing, coupling and changing in accordance with—other form.[51] This is in direct opposition to the truths of the nondual traditions and Spinoza’s real difference, in which the entirety of the world of form arises in strict inter-dependence in its relations with other form. Kant’s ding en sich was (or has become) a numerical identity and difference, an absolutized category free from relation itself, but in absolute opposition to other categories. And so Kant—or the post-Kantians in his name[52]—bypassed all of ontic sub-representational relation—jumping directly from the relative world of representation to the absolute of non-relation—and by default relegating the ontic to the untouchable absolute category of the “noumenon” while freeing up “phenomenon” for further games with suture and scalpel.

And so the real world of sub-representational relation—Brahma—was sunk into the ineffable absolute scope, a lost continent of Philosophy, while the transcendent world of real illusion—Maya—was elevated and venerated as a worthy patient. This veneration itself is indeed deserved (though the operations performed by the doctors of Philosophy may not be). Maya is not only real, but also a real illusion and a real representation. She is more real than Brahma…but only because she is Brahma, in her roots and in her very soul. See Figure 75, below.

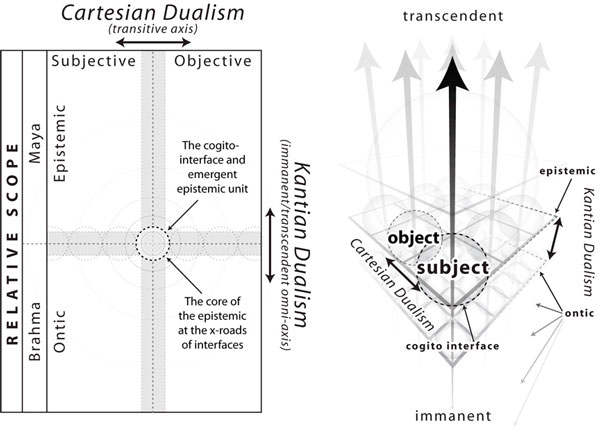Figure 75: Double-Crossing Dualisms: The orthogonal intersection of the Cartesian transitive duality between subject and object and the Kantian immanent/transcendent duality between ontic and epistemic is precisely our crossroads of interfaces, the very core of the epistemic at the cogito-interface itself.

The task of post-Kantian, post-ontotomy Interface Philosophy, then, has been to bring the ontic back out of the absolute scope, and to provide an epistemic interface for exploring this lost continent. And in this process we will continue to demonstrate that the ontic is not the ineffable, untouchable Absolute, but fully within the relative and effable world of form embraced in the very interface of Maya and Brahma. And indeed, this interface of Maya coming to know Brahma grows ever larger as more and more unknown territory is uncovered daily and become known. But more to the point, in our relative freedom to explore the lost ontic continent of Brahma in epistemic union with Maya, we will then be equipped to explore the lofty heights to which only Maya can lift us.

[[Continued in SpinbitZ Volume I: Interface Philosophy, Mathematics and Nondual-Rational Empiricism]]

ENDNOTES

1. Lowest common denominator…

2. The transitive (horizontal) severing of the subject/object polarity, as we will come to understand shortly.

3. The severing of the ontic from the epistemic on the orthogonal or vertical immanent/transcendent omni-axis, as we will see. This is the crossroads of the subject/object and ontic/epistemic polarities, on the transitive- and immanent/transcendent omni-axes, respectively.

4. See the section, Interface Epistemology: A Preliminary Sketch, p541.

5. For the continuation of this metaphor, see the section, Condition Still Critical: Waking Up from the Post-Op Nightmare of the Kantian Radical Ontotomy, p545.

6. … from Daniel Dennett

7. Qtd in Will Durant, The Story of Philosophy.(Durant)

8. See I/T Interfaces, the Omni-Uni and the Omni-Non, p146.

9. Indeed, there is a rampant Foundational metaphysics hidden under much of Science, despite the fact that Foundational truth-claims—a main feature of medieval Philosophy and Theology—have been demonstrated extremely problematic and indeed illegitimate during the last century of Philosophical progress.

10. … or “life-forms” as Wittgenstein called them.

11. Deleuze, Expressionism in Philosophy, p79

12. We’ll see this more explicitly through our “embryogenesis of the concept” in the section Spinoza: A Nondual Sketch, p664.

13. See Spinoza: A Nondual Sketch, p664.

14. ISC call, May 12, 2007

15. Wilber’s limitations here are to be expected of a human being, rather than a god. His net was cast wide and his focus was on the eastern forms of nonduality, not on “Rationalists,” such as Spinoza.

16. Deleuze, Expressionism in Philosophy, p. 38

17. A paradigm is a function of technology, and a philosophical system itself is a technology; an invention based on the industry of language.

18. This is similar to Phillip K. Dick’s conception of God, getting lost in his own creation…and it is ironically similar to the role of the author, as I am right now lost inside this creation as I create it.

19. This is the essence of Deleuze’s conception of Empiricism, an intensely creative and conceptual endeavor coupled always and ultimately with immanent and causal explanations of emergent and sensate reality. That is why he considered Spinoza one of the key empiricists, as opposed to Descartes who imposed his system from the outside, from the limitations of his own mind, rather than recognizing the limits of the mind to grasp the immanent capabilities of matter to be at one with mind as aspects, or attributes, of a single immanent causal reality.

20. See the section on Part Two: Interface Mathematics, p200.

21. A conceptual “symmetry breaking”

22. This is the essence of the concept of the “Aspect Infinite,” which is the 2nd order infinite, found in Spinoza’s Triune Infinite, p270.

23. Interestingly, this was also the period in my life when I was experimenting with the interface between tedium and excitement, or repetition and difference in music.

24. “Oneirology is the scientific study of dreams. The term comes from the Greek oneiro which means dream.” An oneironaut, then, is a creative practitioner, or explorer of dreams.

25. With the adjective form, ‘scalactic’ having a nice sci-fi ring to it.

26. One of the motivations for using the term immanent-transcendent axis, rather than ‘scalaxis,’ is that operationalizing the idea of ‘transcendence’ as a common, and fundamental aspect of reality, will help bring it “down to earth”, so to speak, and help reconcile the transcendent-bias, and immanent-transcendent dualism infecting pre-rational modernity (and post-post whatever).

27. See, Evolution is Involution Seen in Reverse, p580.

28. Notice the modal-centric emphasis on locality, as in the center is everywhere. The law of absolute reversal requires that this polarity be switched to operationalize its inverse. It then becomes “God is an intelligible sphere whose center is nowhere and whose circumference everywhere.” It works from either an inward or an outward perspective.

29. It is clear, however, that an infinitely small distance, were it not a contradiction in terms, would take zero time to cross, which we will explore in greater detail in Interface Mathematics.

30. …and as we will see, the sphere is the most general representation of number, in identical opposition to this same immanent-transcendent axis (the identical opposite of number), The Infinite.

31. Note that we are not concerned here with the use of transitive axes to represent non-spatial, or non-physical aspects, at this point, except for the representational use of the transitive-axis to stand for the immanent-transcendent axis in the main Vision-Logic Coordinate System diagram (two figures above).

32. See, for example, The Univocity Framework (UF), p153.

32. See, Back to Zeno, p448.

34. Recall Figure 7: The Nuclear VCS Diagram With Coordinates:, p144.

35. See, The Nondual-Rational and Empirical Embryogenesis of Mathematics, p217.

36. It is also the polarity of Spinoza’s Substance/God, with omnilocal immanence-in-transcendence equating to Substance, and omni-local transcendence-in-immanence equating to “God.” This last point takes us far afield, but see Leibnoza Von Spinbitz (p659), to jump the line and explore further.

37. We are not here using the term ‘singularity’ in its strictly mathematical and operational sense. Rather, we use the term to highlight the infinity hidden in the “infinitely small” Euclidean point. Indeed, this implicit infinity is the very source of the immanent infinities (mathematical singularities) found when physicists of the early twentieth century tried to calculate the energy of an electron—represented as such a point—as an inverse-squared function of the distance to its center and its non-existent terminating surface.

38. See Exploring the Univocity Framework, p190.

39. This is another aspect of the trans-trans-bias. See The Image of the Trans-Trans-Bias, p312.

40. As Samuel Levey termed it in his article “Leibniz on Mathematics and the Actually Infinite Division of Matter.”

41. For further information, see, for example, Spinoza’s Triune Infinite (p270) and Reconnecting the Lost Thread of Mathematical Rationalism: Spinoza, Leibniz, Immanence and the CalculusReconnecting the Lost Thread of Mathematical Rationalism: Spinoza, Leibniz, Immanence and the Calculus (p400).

42. See the related discussion on The (Binary) Cycle of Unity, p254.

43. See Exploring the Univocity Framework, p190.

44. See Infinite Unity: ALL is ONE, p240.

45.… incorporating in the omni-non the identical opposite necessary at the absolute scope…

46. See Unity and Nonduality (p239), and The (Binary) Cycle of Unity (p254).

47. The I/T omni-axis is, mathematically-speaking, non-operational, due to its taking on of the properties of the absolute scope in its omni-/non-locality. In other words, in order to operate mathematically, one position (ideal point and immanent pole of an I/T axis) from the infinite must be abstracted and selected so as to construct the first number in Operational Mathematics, the volumetric boundary (a real-point). We’ll explore this in much more detail later. See for example Empirical/Experiential Beginnings: Bucky’s “Operational Mathematics” (p217), The (Binary) Cycle of Unity (p254) and The Holarchical Unfolding of Number and Operation (p306).

48. See, for example, The Secret Doctrine, by H.P. Blavatsky or Ken Wilber’s Integral model.

49. See Infinite Unity: ALL is ONE, p240.

50. See, Post-Post-ism-ism: Condition-Critical in the Ontic-Shadow of Post-Kantian Dualism, p40.

51. When asked in person, Fox stated that Kant’s noumenon is not free from relation, but the thing in itself is related to all things. This would then be equivalent to the original Aristotelian notion of the ontos, the One. I then asked him whether Kant made this explicit and the answer was, “No.” It is well known that Kant himself was unclear about his noumenon/phenomenon distinction, and it is the post-Kantian reaction which was likely most responsible for the radical ontotomy discussed herein.

52. There are indeed Kantians who don’t believe this was Kant’s original intent and that it is the result of subsequent misinterpretations. Mr. Fox is one of them. This author has not studied Kant’s original surgical procedure in enough depth to make such a call, but the aftermath is ubiquitous enough in my contact with run-of-the-mill Kantians and quite readily apparent.

Bibliography

Blavatsky, Helena Petrovna. The Secret Doctrine (Reprint edition). Theosophical University PR, 1999.

Clayton, Philip. The Problem of God in Modern Thought. Wm. B. Eerdmans Publishing, 2000.

—. The Problem of God in Modern Thought. Wm. B. Eerdmans Publishing, 2000.

Cooper, David E. Metaphysics. Blackwell Publishing, 2000.

Damasio, Antonio. "Looking for Spinoza." n.d.

Deleuze, Gilles and Felix Guattari. What is Philosophy? Columbia University Press, 1996.

Deleuze, Gilles. Difference and Repetition. n.d.

—. Expressionism in Philosophy: Spinoza. Brooklyn: Zone Books, 2005.

—. Spinoza: Practical Philosophy. San Francisco: City Lights Books, 1988.

Dennett, Daniel. Consciousness Explained. n.d.

Duffy, Simon. "The Logic of Expression in Deleuze’s Expressionism in Philosophy: Spinoza: A Strategy of Engagement." International Journal of Philosophical Studies (n.d.): 47-60.

Durant, Will. The Story of Philosophy. n.d.

Einstein, Albert. "Forward. Reflections and Maxims." Runes, Dagobert D. Reflections and Maxims. New York: Philosophical Library Inc, 1965.

Fox, Claude L. Ph.D. Foundations: A Manual for the Beginning Student of Epistemology. Lanham: University Press of America, 1999.

—. "personal correspondence."

Fuller, R. Buckminster. Synergetics: Explorations in the Geometry of Thinking. Macmillan Publishing Co. Inc., 1975, 1979.

Goetschel, Willi. Spinoza’s Modernity: Mendelssohn, Lessing, and Heine. n.d.

Haserot, Francis S. "Spinoza’s Definition of Attribute." The Philosophical Review 62 (1953): 499-513.

Kant, Immanuel. The Critique of Pure Reason, 2nd Edition. 1787.

Montag, Warren and Ted Stolze, The New Spinoza. Minneapolis : University of Minnesota Press, 1997.

Negri, Antonio. The Savage Anomaly. Minneapolis: University of Minnesota Press, n.d.

Opdenberg, H. R. "Universe of Infinite Variety." Theosophy. 8 July 2006 <http://www.theosophy-nw.org/theosnw/science/sc-opden.htm>.

Spinoza, Baruch. Short Treatise on God, Man and His Well-Being. New York: Philosophical Library, Inc., 1958.

Spinoza, Benedict De. Ethics; On the improvement of the Understanding; Correspondence. New York: Dover, 1955.

Staloff, Darren. Great Minds of the Western Intellectual Tradition: Lecture 12: The Philosophy of G.W. Leibniz: Audio CD Lecture: The Teaching Company. n.d.

—. Great Minds of the Western Intellectual Tradition: Lecture 33: Spinoza—Rationalism and the Reverence for Being: Audio CD Lecture: The Teaching Company.

Stewart, Matthew. The Courtier and the Heretic: Leibniz, Spinoza, and the Fate of God in the Modern World. New York: Norton, 2006.

—. The Truth About Everything: An Irreverent History of Philosophy with Illustrations. New York: Prometheus Books, 1997.

Surin, Kenneth. "Spinoza, Baruch." Parr, Adrian. The Deleuze Dictionary. Ed. Adrian Parr. New York: Columbia University Press, 2005. 260-2.

Verelst, Karin and Bob Coecke. "Early Greek Thought and Perspectives for the Interpretation of Quantum Mechanics: Preliminaries to an Ontological Approach." CLEA-FUND, Free University of Brussels (n.d.).

Verelst, Karin. "Some remarks on the relation between the microcosmical and macrocosmical." CLEA, Free University of Brussels (n.d.).

—. "Zeno's Paradoxes. A Cardinal Problem: I. On Zenonian Plurality." FUND-CLEA Vrije Universiteit Brussel (n.d.).

Watson, Burton, trans. The Lotus Sutra. n.d.

Watts, Alan W. The Joyous Cosmology. New York: Pantheon, 1962.

—. The Two Hands of God. n.d.

Wilber, Ken. A Brief History of Everything. Boston: Shambhala Publications, 1996.

—. Integral Spirituality. Boston: Integral Books, 2006.