|
TRANSLATE THIS ARTICLE
Integral World: Exploring Theories of Everything
An independent forum for a critical discussion of the integral philosophy of Ken Wilber
 Donald J. DeGracia
Donald J. DeGracia, Ph.D., is Associate Professor at the Wayne State University Department of Physiology. Dr. DeGracia studies the mechanisms of cell death following brain ischemia and reperfusion. This clinically relevant research models brain injury that occurs following stroke or following resuscitation from cardiac arrest. The main focus of this work is the causes and consequences of reperfusion-induced inhibition of protein synthesis. See also his metaphysical website and his blog dondeg.wordpress.com. Evolution: Chance
or Dynamics?
Donald J. DeGracia

Ken Wilber's recent statements about love and membranes being the driving force for structure formation in the universe have stimulated discussion about how this notion more resembles creationism than evolutionary theory. However, the discussions about evolution[1] are rather dated. We would here like to briefly describe current and state of the art ideas that are emerging in the field of evolution to account for biological structure. Our key source is a 2004 article by Sui Huang entitled: Back to the biology in systems biology: What can we learn from biomolecular networks? (which can be downloaded in full here[2]).
Too Many States
The fact is, the idea of chance and probability in evolution of life is problematic. Consider, for example, the problem of protein folding. The Levinthal paradox states that “if a protein were to fold by sequentially sampling all possible conformations, it would take an astronomical amount of time to do so, even if the conformations were sampled at a rapid rate”.[3]
The specific three dimensional shape of a protein is known as its conformation. A single protein is a polymer composed of amino acids. An average protein might consist of 500-1000 amino acids. There are, as stated above, an astronomical number of possible allowed (non-covalent) bonding interactions between the amino acids. A given set of specific bonding interactions will produce one of the astronomical number of possible conformations of the protein. If the bonding interactions are treated probabilistically, then there are so many possible interactions that, as the Levinthal paradox states, it would simply take too long for each of these states to be sampled, and the final 3D conformation of the protein would, effectively, never occur.
However, proteins fold into their correct conformations typically on the time scale of seconds or minutes. Thus other factors must impinge and alter the system from one of simple probabilities and chance.[4]
An analogous problem holds when one considers the idea that chance mutations provide the raw materials upon which natural selection operates. It is well known today in modern molecular biology that only a relatively small percentage of the genetic material codes for the amino acid sequence of a protein. Other sequences in the chromosomal DNA code serve as regulatory regions that specify the conditions under which a gene is transcribed (e.g. converted to mRNA and then to protein). The regulatory sequences participate in a bewildering array of regulator interactions including binding of transcriptional activators or repressors, transcription termination sequences, splicing sites, so-called “epigenetic” modifications such as DNA methylation and so on.
From the moment a sperm meets an egg, an extraordinarily complex set of processes are triggered that lead to a highly orchestrated process of cell division and differentiation that culminates ultimately in the mature form of the organism. Needless to say that, in spite of literally tons of books and journal articles about these developmental processes, they are at best poorly understood today.[5]
Thus, when we consider the idea of chance mutations, we are talking specifically about a change at a random location in the DNA that in turn will affect either the structure of a protein or an alteration to the complex and poorly understood regulatory processes that underlie the orderly development of an organism from a sperm and an egg. When viewed from a purely probabilistic point of view, the odds are overwhelmingly in favor that any random mutation will negatively affect the development of an organism, resulting in a developmentally defective and likely aborted organism.[6]
Said simply, the odds that a random mutation will result in a defective or dead organism are large. The odds that a random mutation will be neutral are also high because it is well known that there are many alternative means to achieve the same end encoded in the developmental process.[7] However, the odds that a random mutation will alter the structure of the organism to allow it to enter a new niche or become a new species reproductively isolated from the parent and survive are almost zero.
Thus, the protein folding and the evolution by random mutation problems have the same form: one is confronted with a complex system that has literally millions of allowed states where most of them are functionally useless.
Reductionism vs. Holism
Now, there is an underlying metaphysic[8] to considering it legitimate to conceptualizing protein folding or evolution in purely probabilistic terms. Huang (2004) describes this as a reductionistic '(localist') mentality in modern biology which stands in contrast to a holistic (or 'globalist') approach to biology. These extreme positions can be characterized by the following difference. To a reductionist, the whole equals the sum of its parts. To a holist, the whole is greater than the sum of its parts. Again, these are not merely philosophical distinctions, but are viewpoints that have practical and technical consequences for how the respective camps do and perform science. The crucial difference is this: if one assumes the whole equals the sum of the parts, one assumes the parts do not interact significantly. On the other hand, for the whole to be greater than the parts implies that the parts do interact significantly. Such interactions will give rise to unexpected behaviors (unexpected from the point of view of how the parts behave in isolation).
If the properties of a protein are only seen as the sum of the properties of the individual atoms of which it consists, then it is legitimate to consider all possible binding states as equivalent. That is, one can assign a probability to each separate state and treat the problem using classical statistics. Likewise, if an organism is simply the sum of the genes encoded in the DNA, then all random mutations are equivalent in that each can be assigned a probability and treated with classical statistics. However, as stated above, this approach does not work. In the case of protein folding it produces Levinthal's paradox.
Clearly, given that probability does not work in either case, there must be some fundamental flaw or blind spot in this reductionistic position. We noted this blind spot above. The parts of the system do interact. This in turn gives rise to novel system properties, sometimes called “emergence”. However, there is nothing mysterious about this process of emergence. It is understood by accounting for the component interactions. The vehicle used for this understanding is the mathematics of networks.
Networks and their Dynamics
It is beyond our scope here to explain network dynamics in great detail. Huang (2004) presents such discussions geared to educated laymen. Here we only outline the salient concepts.
A network consists of nodes that are interconnected via links (sometimes called edges). Links describe functional interactions between the nodes. In the simplest cases, the links may represent functions such as activation or suppression. Every node in the network has a state. The simplest type of network is a Boolean or binary network in which the state of a node is either on (1) or off (0). A list of the state of every node in the network is called the network state vector or configuration. The number of possible configurations increases rapidly with addition of nodes. For example, a network of 100 binary nodes has up to 2100 configurations.
Treating 2100 configurations probabilistically will give rise to “astronomical” numbers of states that will not resolve in realistic time frames. However, networks offer an alternative understanding. In a network, most of the configurations are unstable. They are unstable because they violate the rules embedded in the links. A very simple example can illustrate these properties. The following quotes from DeGracia (2010):[9]
“In a networked view of cell function, the various component parts of the cell, be these proteins, genes, mRNA molecules, signal transduction molecules, etc. are represented as individual nodes in a network. In a Boolean network each node has only two states: on (=1) or off (=0). How can a network whose nodes are either only on or off be biologically relevant? Consider that a node, let's call it “A,” represents an enzyme. One may associate the node being “on” (A=1) with the active state of the enzyme, and the node being “off” (A=0) with the inactivate state of the enzyme. Similarly, if a node represents a gene, then the node on would correspond to transcription of the gene, and the node off would mean the gene is not being transcribed.”
“Interactions of the individual nodes are depicted by links or edges which capture some facet of the relationship between the nodes… The [links] constitute a set of rules to determine the state of a node… Returning to our example enzyme A, consider that A has two inputs, call them B and C, where B is an activator and C an inhibitor of A (Figure 1). If B is active (=1), then A is also active (=1). However, if C is active (=1), then A is inactive (=0). A binary contingency table can be devised that [lists the allowed] combinations of inputs on the node and how these then determine the node's state.”
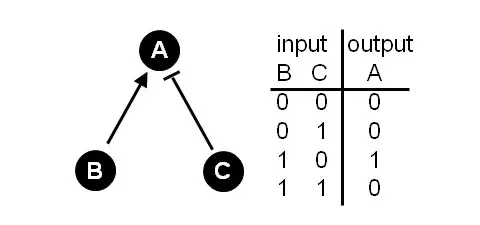 Figure 1: A simple 3 node network.
Figure 1: A simple 3 node network.
Right: Contingency table describes the allowed or stable network states.
Figure taken from DeGracia (2010) and used under Journal Open Access Policy[10].
One can see by looking at Figure 1 the logic of networks. All of the entries in the contingency table make sense. If both B and C are inactive, then A is also inactive. If C, the inhibitor, is active, then A is inactive. If B, the activator is active, then A is also active. If both the inhibitor (B) and activator (C) are active, they will cancel out and A will be inactive.
However, one can immediately see examples of unallowed states. You cannot have [B,C,A] = [0,1,1]. This would correspond to the inhibitor being active and A also being active. It is simply a logical contradiction. Similarly one cannot have the state [B,C,A] = [1,0,0]. This would correspond to the activator (B) being active, but A being inactive. In short, the unallowed, or unstable, states violate the rules inherent in the network.
Thus, only certain states are allowed by the network. The allowed states are precisely a consequence of the structure of the network. This fact that, by its very structure, a network allows some states and disallows others is what Huang (2004) refers to as “intrinsic constraints.” It is the notion of intrinsic constraints that provides an expanded view of the nature of evolution.
Networks Impart Intrinsic Constraints to What Evolution Can Do
Although only a simple example is given above, one can multiply this example in their mind and expand the network to an arbitrarily large size. No matter how large the number of nodes and their interactions, the network structure itself will exert a kind of top-down control over the possible changes of the individual nodes. Such notions are changing the face of modern biology. The reductionistic approach has its place, and its place is not in explaining the global features of biological systems. The old nursery rhyme is apt here:
“All the King's horses and all the King's men couldn't put Humpty together again.”
Reductionism excels at allowing us to understand the pieces, the components, of biological systems. Reductionism fails miserably when it comes to putting the pieces back together to understand how the system as a whole works. Hence, the rise of network logic in biology. The technical holism of network formalisms has wide-ranging applicability. It can be used to explain development, gene interactions, cell injury, and evolution (see citations in Huang 2004).
What the network view provides are the following insights. Biological systems are instantiations of networks. Networks describe the global operating characteristics of complex systems. It does so by understanding the network dynamics. The dynamics are how the system changes as a function of time, specifically how the network changes configurations from instant to instant. Since only some configurations are allowed and others are disallowed by the very structure of the network, one can readily determine the changes in time from more unstable to less unstable states of the network. These constitute the allowed paths of change that are intrinsic to the very structure of the network.
When applied to evolution, these insights in fact provide a new mechanism by which to understand how evolution works. Evolution is intrinsically constrained by the structure of the pre-existing system. In other words, the loss or gain of features and functions in an organism, including gross anatomical changes, will only occur if they are consistent with the network dynamics. Further, gross anatomical changes will be most expected to occur at bottle neck nodes in the developmental process. A bottle neck node is one that is an important branch point in the determination of the body plan, for example, whether there will be two arms and two legs, or 6 legs (as in a spider).
What this view means is that not any old random mutation will contribute in a progressive fashion to evolution. As is even clearer once the notion of networks is presented, any random mutation will either be neutral or negative, that is, have no effect on, or negatively affect the behavior of the network.
Thus, as Huang (2004) states more fully and more elegantly than I have here, it is likely that evolution by intrinsic network constraints is a much more important factor than selection by random mutation is the production of new species.
How Does This Parse with Wilber's View?
Hopefully this short introduction to the application of networks to biological systems has at least made plain that there are rational and logical views in modern biology that have the power to deal with the complex nature of biological systems. There is nothing mysterious whatsoever about networks and their dynamics. The networks are simple algebraic mathematical constructs. Understanding their dynamics involves differential equations. If there is any mystery going on here, it is the time-worn mystery of why mathematics works so well at describing the physical world.[11] Additionally, because these are mathematical approaches, they are not limited to application in only the field of biology. One can speak of the dynamics of chemical systems, of chemical networks and so on.
One might be tempted to associate Wilber's mysterious “membrane” with the intrinsic dynamics of the system under consideration. However, as we have seen, this has nothing whatsoever to do with probability and chance. Nor is it literally a boundary as a membrane is. But the intrinsic constrains of the network dynamics are a bounding structure that limits the allowed states of the complex system. The network view is a palliative to the reductionist who has painted himself into an intellectual corner by using only classical probability theory to deal with complex systems.
However, it is not wise to put words in Mr. Wilber's mouth, and we probably should assume that such notions did not guide his use of the membrane metaphor.
Where “Eros” or “Love” fit in is, essentially… nowhere. The variety of forms of love itself, as felt by humans, can now be understood as specific configurations of the complex networked structure we call the human nervous system. It is rather difficult to see how this specific set of brain configurations can drive processes (e.g. chemical and biological evolution) that are, effectively, isolated from human brains in both space and time.
However, there is a great irony here. Wilber, who has spent his career trying to re-“spiritualize” the Western intellect, is missing a most fundamental point. In John 1:1 it is said: “In the Beginning, God had the Logos”. God had the “Logic”, the logic that created and sustains the Cosmos. It would seem that the Logos seems to express itself via mathematics in the human realm. There are no membranes, there is no love, and it is not chance or probability. The facts of physical experience map to ever greater degrees to mathematics. Many practicing mathematicians have openly expressed their adherence to the Pythagorean philosophy of math[12] that there is indeed an objective (in some sense) world of ideal forms of which our physical world is but an imperfect reflection.
Conclusion
Hopefully this article has increased the reader's appreciation of the exciting things occurring in modern biology, and more broadly, in modern mathematics. Science does not sit still. New ideas are emerging at an exponential pace. There is no need to get caught in the old debates of a Dawkins or Gould. The emerging ideas of complex systems provide both technical and intellectual tools to tackle systems that were poorly understood even 10 or 20 years ago. And falling back on nebulous and emotionally-charged language to describe our vast and mysterious Cosmos is an insult to the majesty and magic inherent in the very concept.
CITATIONS
DeGracia (2010). Towards a dynamical network view of brain ischemia and reperfusion. Part I: background and preliminaries. J Exp Stroke Transl Med. Mar 15; 3(1).
Huang (2004). Back to the biology in systems biology: What can we learn from biomolecular networks? Briefings In Functional Genomics And Proteomics. February 2(4). 279-297.
NOTES
[1] David Lane, "Frisky Dirt", http://www.integralworld.net/lane19.html and Frank Visser, "Arguments from Ignorance", http://www.integralworld.net/visser41.html.
[2] Sui Huang, "Back to the biology in systems biology: What can we learn from biomolecular networks?", http://www.childrenshospital.org/research/huanglab/PDFs/Huang_%20BFGP2004.pdf
[3] "Protein folding", http://en.wikipedia.org/wiki/Protein_folding
[4] To conclude the story, there are now known to be entire subcellular systems necessary for the proper folding of proteins into their mature 3D form. These collectively are known as “chaperone” systems, and even these are only part of the story.
[5] As an aside, these considerations relate to the public debate on stem cells: their basic biology is barely understood, and much of what is heard about stem cells as cures for stroke or Alzheimer's disease in the media is mere hype.
[6] Only roughly 8% of conceptions following sex result in formation of an organism. 92% lead to premature abortions, naturally. Further, a very large percent of the population carry some defect in their organs due to faulty development such as having only one kidney, or the holes in the heart not closing completely.
[7] This insight stems from the experience with genetic knockouts where some gene is excised from the organisms' genome. In many cases, gene knockouts have no overt effect, indicating that some redundancy replaces the knocked out function. On the other hand, other genetic knockouts are known as “embryonic lethal” meaning the organism dies before development is complete.
[8] We mean this is a philosophical sense, but only insofar as it affects one's technical and scientific approach, as detailed in Huang (2004).
[9] Donald J. DeGracia, "Towards a dynamical network view of brain ischemia and reperfusion. Part I: background and preliminaries", http://www.jestm.com/index.php/jestm/article/view/46/147
[10] "Open Access Policy", http://www.jestm.com/index.php/jestm/about/editorialPolicies#openAccessPolicy
[11] See for example, "Mathematics and the physical world", http://www.gap-system.org/~history/HistTopics/World.html or "Mathematics and the Physical World", http://www.rasit.org/files/MathematicsPhysical.htm.
[12] Such greats as Georg Cantor or Kurt Gödel fall into this camp.
|
 Donald J. DeGracia, Ph.D., is Associate Professor at the Wayne State University Department of Physiology. Dr. DeGracia studies the mechanisms of cell death following brain ischemia and reperfusion. This clinically relevant research models brain injury that occurs following stroke or following resuscitation from cardiac arrest. The main focus of this work is the causes and consequences of reperfusion-induced inhibition of protein synthesis. See also his metaphysical website and his blog dondeg.wordpress.com.
Donald J. DeGracia, Ph.D., is Associate Professor at the Wayne State University Department of Physiology. Dr. DeGracia studies the mechanisms of cell death following brain ischemia and reperfusion. This clinically relevant research models brain injury that occurs following stroke or following resuscitation from cardiac arrest. The main focus of this work is the causes and consequences of reperfusion-induced inhibition of protein synthesis. See also his metaphysical website and his blog dondeg.wordpress.com.
