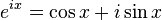|
TRANSLATE THIS ARTICLE
Integral World: Exploring Theories of Everything
An independent forum for a critical discussion of the integral philosophy of Ken Wilber
 Elliot Benjamin is a philosopher, mathematician, musician,
counselor, writer, with Ph.Ds in mathematics and psychology and the author of over 230 published articles in the fields of humanistic and transpersonal psychology, pure mathematics, mathematics education, spirituality & the awareness of cult dangers, art & mental disturbance, and progressive politics. He has also written a
number of self-published books, such as: The Creative Artist, Mental Disturbance, and Mental Health. See also: www.benjamin-philosopher.com.
SEE MORE ESSAYS WRITTEN BY ELLIOT BENJAMIN
The Mathematical Universe, Science, and Euler's Formula
A Response to Andy Smith's Review of Mike Hockney's
"The Mathematical Universe" and to Rolf Sattler's article
"Rupert Sheldrake and Dogmatism in Mainstream Science"
Elliot Benjamin
It seems to me that Hockney, and Andy Smith, are attributing far too much significance to Euler's formula than is warranted.
I always appreciate Andy Smith's Integral World articles, and his latest long review of Mike Hockney's The Mathematical Universe [Getting to the Point] is no exception [1]. Although I have not read Hockney's book, the tremendous emphasis upon mathematics as the essential meaning and driving force of the origin of the universe, as Smith has described Hockney's thinking skillfully with impressive detail and analysis, has captured my interest. In my end of 2013 Integral World philosophy of mathematics debate with Peter Collins [2], I emphasized the validity of pure mathematics as an aesthetic art form in its own right, without the need of practical application to justify its existence. From the way that Smith describes Hockney's passionate emphasis upon mathematics as the driving force of the universe, this reminds me very much of Peter Collins' perspective on mathematics. For Collins we have the Riemann Hypothesis as the guiding force of the universe, and it seems that for Hockney we have Fourier analysis and Euler's formula for the same purpose (cf. [1], [2]).
Being a pure mathematician and not an applied mathematician, admittedly I do not know much about how far-reaching and extensive is the practical significance of the sine and cosine waves that Hockney apparently sees as the be-all and end-all of existence (cf. [1]). Of course as a mathematician I could point out that not just “any” function can be approximated by Fourier trigonometric series, but rather only “nice” functions that are “piecewise continuous.” However, part of what I want to emphasize in this article is that it seems to me that Hockney is attributing far too much significance to Euler's formula than is warranted. In fact, I must say that even Andy Smith appears to me to be attributing more significance to Euler's formula than is warranted. I will explain this shortly (mathematically), but first I want to make a few remarks related to Smith's analysis of Hockney's putting “reason” on a pedestal, and also make a few remarks in response to a recent Integral World article by Rolf Sattler entitled Rupert Sheldrake and Dogmatism in Mainstream Science [3].
There are some scientists who criticize our current mainstream scientific beliefs, ranging across everything from quantum physics to relativity to natural selection to the origin of life to the Big Bang theory of the origin of the universe. Rupert Sheldrake is certainly in this category of scientists who are critical of mainstream science—in his case in the field of biology, and apparently Rolf Sattler joins this group as well—specifically in his biological field of plant morphology (cf. [3], [4]). I myself am quite interested in reading about alternative theories to our current mainstream science beliefs—especially in regard to the origin of the universe, as I must agree with Hockney (as described by Smith) that the Big Bang doesn't say anything about what was there “before” the Big Bang to have caused the Big Bang. When I use my own mathematical reasoning abilities, what I come up with is that the most “reasonable” hypothesis to me is that there was something that was “always” there—meaning some kind of “energy” that we have no conception of. Otherwise we get an infinite regress into “what caused what” and we always end up with “but where did this come from?”
Now there are conceptions in quantum physics of how “something can come from nothing,” but when I read about this it seems to me that the “potential something” was already inherent in the vacuum or nothingness, at least as far as I can understand what I am reading [5]. So where did this “potential something” come from to begin with? This is one area of philosophical speculation for me—and I must admit that when I think in these terms what I come up with is not too far removed from some kind of “intelligence” that somehow was involved in the transformation of this “potential something” into an “actual something.”
When I look at our current mainstream science alternatives, I find that my choices are—for lack of a better world—preposterous.
But a primary reason why I come up with this conclusion is that when I look at our current mainstream science alternatives, I find that my choices are—for lack of a better world—preposterous. There are all kinds of “very weird” theories in physics that have never been verified or observed as far as I know—such as dark matter, dark energy, black holes, “strings,” and most especially—parallel universes (cf. [5]). According to John Bockris, a well-respected physical chemist who worked against the scientific mainstream for many years to finally successfully introduce his ideas about “cold fusion”, these theories have been developed to justify our current scientific quantum physics/Big Bang theory of the formation of the universe, as one of our biggest puzzles that origin of life scientists find extremely unsettling is how the universe was “fine-tuned” with all the physical laws of the universe and mathematical constants being “just right” for life to evolve on our planet [6]. Suffice it to say that the likelihood of this happening is so astoundingly remote that our current established scientific thinking embraces the “many worlds” (also known as “parallel universes”) theory to account for the statistical probability of our planet eventually forming life (cf. [5], [6]). Perhaps I am just old-fashioned and conservative, but I must say that I do not see a “many worlds” hypothesis as being any less bizarre and unlikely to be the “truth” than an “intelligent design” hypothesis. And I will go out on the limb and admit that if I were “forced” to choose between the two, I would choose ID.
Before changing gears and giving you the mathematical formulation of Euler's Formula that I said I would include here, let me say a few words related to Sattler's defense of Sheldrake as a legitimate scientist, and particularly in reference to Sheldrake's work in the area of parapsychology (cf. [3], [4]). I am in agreement with Sattler that although EvoDevo has contributed a great deal to our understanding of how evolution works, it does not help us in explaining some of the more controversial areas of scientific investigation, in particular the area of parapsychology. Sattler mentions two of Sheldrake's parapsychology experiments, involving dogs who appear to “know” when their masters are coming home, and the sense of knowing when someone is staring at you when you are not able to see them (see [3] for a listing of Sheldrake's relevant books here). However, this is just the tip of the iceberg, as there are a great many quantitative scientific studies that have been made in the area of parapsychology over the past 150 years, a number of which I believe are of high quality scientific caliber, due in large part to the challenge of skeptics to improve upon the scientific design of these experiments. Bockris includes an excellent description of the wide scope of this parapsychology research (cf. [6]), and I will reference here a selection of peer-reviewed parapsychology publications that includes the controversial areas of healing at a distance, physiological correlations at a distance, telepathy and ESP, mind-matter interaction, general overviews and critiques, as well as some areas that are even “more controversial,” such as precognition and presentiment (knowing the future before it happens) and most especially survival of consciousness (i.e. life after death) [7].
Perhaps you may wonder why more of these publications have not made it into mainstream science publications if they are of such high quality (there are a few of them that have). I think that Sattler, Sheldrake, and Bockris, as well as radical physicist/retired engineer Ron Pearson, give us a good indication of some of the artificial barriers that mainstream science puts up to guard against ideas that could shake the foundations of established science (cf. [3], [4], [6], [8]). However, “entanglement” of subatomic particles at great distances from one another is part and parcel of quantum physics theory, and there are theories of how this kind of entanglement could generalize to human beings through biological mechanisms such as microtubules (cf. [5], [7]). Perhaps it would suit us well to follow Sattler's advice and not refer to these parapsychology ideas as “new” but rather as “generalizations of the quantum theory of subatomic particles.”
 Leonhard Euler
Leonhard Euler
Well I think it's now time to shift gears and once again put on my mathematical hat. Given that I have put myself in the somewhat dubious situation of admitting that I see more merit in “intelligence” than in “many worlds” to explain the formation of our planet to eventually host life, let me see if I can somewhat redeem myself by at least giving you a mathematical explanation of how Euler's formula is very much a “constructed” formulation that I think Hockney—and even Andy Smith—are giving too much importance to in regard to over-estimating just how much complication is involved here. I'll try to be brief, but it does require some mathematics to explain—in particular some Trigonometry and Calculus—so please try to stay with me here as the end result I think will be well worth it.
Euler' formula states that:
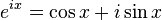
...where i is the imaginary number the square root of -1 and e is the irrational number (non-repeating and non-terminating decimal) that is approximately 2.718281828.... Euler's formula is all based on infinite series, which is generally taught at the end of the first year of Freshman Calculus. One learns that by applying Taylor series, the infinite series of cos x about the point x = 0 can be written as 1 – (1/2)x2 + (1/4!)x4 – (1/6!)x6 + ...where n! means “n factorial” which is the product of all the consecutive natural numbers from 1 to n; thus for example 2! = 2 x 1 = 2, 4! = 4 x 3 x 2 x 1 = 24, and 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 (the symbol x as I am using it in this context represents multiplication, and I think it will be obvious to you when I am using the symbol x in this context below). The dots signify that the pattern continues infinitely, and I don't want to overdo this mathematical exposition with messy formulas, but they are easily accessible in any standard first year Calculus textbook. In a similar way, we can write the Taylor series for sin x about x = 0 as x – (1/3!)x3 + (1/5!)x5 – (1/7!)x7 + ..., and for ex about the point x = 0 as 1 + x + (1/2)x2 + (1/3!)x3 + (1/4!)x4 + ...
Well Euler's formula says something about a complex exponent, where exponent is the power we raise numbers to. For an ordinary natural number, we have for example 32 = 3 x 3 = 9, 25 = 2 x 2 x 2 x 2 x 2 = 32, 104 = 10 x 10 x 10 x 10 = 10,000, etc. I again want to not overdo my mathematical exposition, but in high school algebra we learn how to take negative exponents and fractional exponents, and it turns out we can formulate “real” but “irrational” (which also means not expressible as a fraction) exponents, such as 3√2, as approximations of fractional (or equivalently decimal) exponents; in other words we can form successive approximations of √2 as 1.4, 1.41, 1.414, etc. and then take 3 to each of these powers using standard fractional exponents, and finally obtain 3√2 as the limit of these approximations.
Let me cut to the chase now and let's talk about imaginary exponents. What possible sense does it make to define for example the imaginary exponent i = √-1? Well this is exactly where infinite series comes to the rescue, and yes it was an ingenious idea by Euler but I think it falls short of the supreme place of importance that Hockney has placed upon it. Euler's idea is as follows: simply substitute i for x in the above formulas I gave you and see what you come up with. We get ei = 1 + i + (1/2)i2 + (1/3!)i3 + (1/4!)i4 + ... and now evaluate what these exponents of i actually are. Since i = √-1, then i2 must equal -1 since squaring a square root gives us what is inside the square root—by definition. Then taking i to the third power means multiplying i2 by i which gives us –i, and taking i to the 4th power is the same as squaring the square of i, which means (-1)2 = 1 (this is all standard high school algebra of exponents). Notice that this process repeats indefinitely; for example i5 = i x i4 = i x 1 = i, i6 = i2 x i4 = -1 x 1 = -1, etc.
But since Euler's formula deals with eix let's now substitute ix for i and see what this gives us. Continuing our series a few more terms we end up with eix = 1 + ix + (1/2)(ix)2 + (1/3!)(ix)3 + (1/4!)(ix)4 + (1/5!)(ix)5 + (1/6!)(ix)6 + (1/7!)(ix)7 + ...And using the basic law of exponents that says (ab)n = (an)(bn) (i.e. the product of two numbers to an exponent is the product of each number to that same exponent), along with the above formulation of i to exponents, we obtain that eix = 1 + ix – (1/2)x2 - i(1/3!)x3 + (1/4!)x4 + i(1/5!)x5 –(1/6!)x6 –i(1/7!)x7 + ...
Finally let's evaluate cos x + i sin x using the above infinite series formulations for cos x and sin x. We obtain the following: 1 – (1/2)x2 + (1/4!)x4 – (1/6!)x6 + ... + i(x – (1/3!)x3 + (1/5!)x5 – (1/7!)x7 + ...If we multiply the second part of this series by i and order this series according to the increasing exponents of x we obtain 1 + ix – (1/2)x2 – i(1/3!)x3 + (1/4!)x4 + i(1/5!)x5 – (1/6!)x6 –i(1/7!)x7 + ... Notice that this matches exactly our above infinite series formula for eix and lo and behold we have just obtained Euler's formula!
Now I am not saying that this is all “easy” or that it was not an ingenious idea of Euler to come up with this. But keep in mind that this is all taught at the end of Freshman Calculus, or is at least presented in standard Calculus textbooks. The whole notion of a complex exponent is actually quite an artificial construct, but we can make sense of it by using infinite series, which as a mathematician I find to be a wonderfully creative and stimulating idea. But there have been many ingenious and creative ideas in mathematics, and though admittedly I am not an applied mathematician and perhaps I don't appreciate just how special Euler's formula is for the context of the origin of the universe, I at least wanted to give Integral World readers a taste of how this formula has been established.
References
1) See Andy Smith (2014), Getting to the Point: A Review of Mike Hockney's The Mathematical Universe at www.integralworld.net; and Mike Hockney (2014), The Mathematical Universe. Hyperreality Books
2) See Peter Collins' (2013) three-part series of essays entitled Dynamic Nature of the Number System, my (2013) response article The Art Form of Mathematics, and our follow-up response articles to each other at www.integralworld.net
3) See Rolf Sattler (2014), Rupert Sheldrake and Dogmatism in Mainstream Science at www.integralworld.net
4) See Rupert Sheldrake (2012), The Science Delusion: Freeing the Spirit of Enquiry. London: Coronet.
5) See for example Steven Hawking & Leonard Mlodinow (2012), The Grand Design. New York: Bantam Books; Lawrence Krauss (2012), A Universe from Nothing: Why There is Something Rather Than Nothing. New York: Free Press; Fred Alan Wolf (2013), Time Loops and Space Twists: How God Created the Universe. San Antonio, Texas: Hierophant Publishing.
6) See John Bockris (2004), The New Paradigm: A Confrontation Between Physics and the Paranormal Phenomena. College Station, Texas: D & M Enterprises Publisher.
7) See www.deanradin.com/evidence/evidence.htm
8) See Ron Pearson (2010), Physics Proves God: The Weapon Forged to Destroy Atheism! Defusing the Conflict with Science at www.Lulu.com
|
 Elliot Benjamin is a philosopher, mathematician, musician,
counselor, writer, with Ph.Ds in mathematics and psychology and the author of over 230 published articles in the fields of humanistic and transpersonal psychology, pure mathematics, mathematics education, spirituality & the awareness of cult dangers, art & mental disturbance, and progressive politics. He has also written a
number of self-published books, such as: The Creative Artist, Mental Disturbance, and Mental Health. See also: www.benjamin-philosopher.com.
Elliot Benjamin is a philosopher, mathematician, musician,
counselor, writer, with Ph.Ds in mathematics and psychology and the author of over 230 published articles in the fields of humanistic and transpersonal psychology, pure mathematics, mathematics education, spirituality & the awareness of cult dangers, art & mental disturbance, and progressive politics. He has also written a
number of self-published books, such as: The Creative Artist, Mental Disturbance, and Mental Health. See also: www.benjamin-philosopher.com.