|
TRANSLATE THIS ARTICLE
Integral World: Exploring Theories of Everything
An independent forum for a critical discussion of the integral philosophy of Ken Wilber
 Andrew P. Smith, who has a background in molecular biology, neuroscience and pharmacology, is author of e-books Worlds within Worlds and the novel Noosphere II, which are both available online. He has recently self-published "The Dimensions of Experience: A Natural History of Consciousness" (Xlibris, 2008). Andrew P. Smith, who has a background in molecular biology, neuroscience and pharmacology, is author of e-books Worlds within Worlds and the novel Noosphere II, which are both available online. He has recently self-published "The Dimensions of Experience: A Natural History of Consciousness" (Xlibris, 2008). SEE MORE ESSAYS WRITTEN BY ANDY SMITH
Lockdowns may not always be necessary, but overwhelming evidence shows that they can dramatically reduce transmission of the virus, to an extent not usually achieved with less restrictive measures.
When Scientists DissentThe Minority View of the PandemicPart 1: Do Lockdowns Work?Andy Smith
Lockdowns are clearly an extreme measure, a last resort, when a contagious and for some, deadly, virus, can't be controlled.
In a long series of highly informative and insightful posts, Frank Visser has explored—-and rebutted—the false claims and profoundly anti-scientific conspiracy theories that have sprouted up in response to the coronavirus pandemic. The ignorance expressed by some of these views is truly staggering and depressing. It has been claimed by one theory or another that there is no coronavirus; that COVID-19 has resulted from electromagnetic emissions from 5G towers; that PCR tests don't work; that the pandemic was intentionally begun to justify a vaccination program that would insert a microchip into everyone, bringing them under control of some world-wide conspiracy; and on and on and on. Why do such claims take root, and garner thousands, millions, of followers? There are many reasons that I won't attempt to enumerate and discuss here, but one important factor is that there are many legitimate areas of disagreement even among scientists, which can be exploited by those who want to cast doubt on the entire profession. Long before the pandemic, we have seen this approach used against evolutionary theory. A large fraction of the population, particularly in the U.S., does not accept the fact of evolution, and propagates alternative views such as Creationism or Intelligent Design. One of the most widely used arguments they employ is that scientists themselves question evolution. It's true that scientists disagree over the various processes involved in evolution. For example, while Darwinism—random variation and natural selection—is widely accepted as the major driving force of evolution, there are other processes that may be involved to some degree, such as self-organizing phenomena, epigenetic inheritance, group selection, and many others. None of the scientists who argue on behalf of these factors deny the reality of evolution; they're simply questioning how it occurred, to what extent processes other than Darwinism may play a role. But this distinction easily gets lost—or is intentionally ignored—by those who do reject evolution. The COVID-19 pandemic provides exceedingly fertile ground for this approach, because the pandemic is, of course relatively new, with the first cases having been reported a little more than a year ago. Scientists have learned much about the virus and the disease during this period, but there is also a great deal that they don't know, or which is controversial. These areas of ignorance, or of disagreement, at best, fuel serious questions about the policies we should take to respond to the pandemic; and at worst, are used by the fringe conspiracy theorists to claim that nothing that scientists say is credible. To take just one example, controversy over the value of masks in reducing the transmission of the virus has encouraged many people to believe that mask mandates are not simply unnecessary, but proof that the government is using the pandemic (if it didn't actually create it), to extend its control over its citizens. In this article, and in some planned subsequent articles, I will discuss some of these areas of scientific disagreement. My purpose in doing this is mostly to address the former, not the latter, problem that I just mentioned. That is, these disagreements have enormous consequences for our political and social responses to the pandemic, so we need to have the best information available to design and implement these responses. I am less interested in discussing these issues as a means to demonstrate the validity of science in general. I say this not because it isn't important to support and confirm scientific advances, but because I seriously question whether anything I say will affect the beliefs of conspiracy theorists at all. Rules of disorderWhat are these areas of scientific disagreement? To begin, we can again draw a parallel with evolution. Just as there is a single dominant paradigm—Darwinism, modified and extended by the so-called new synthesis—there is a dominant scientific view of COVID-19. Just as virtually all scientists accept Darwinism in its broad outlines, essentially all of them accept the dominant view of COVID-19. The main tenets of this view are that:
No rational, informed person, let alone anyone worthy of being called a scientist, disagrees with any of these points (except possibly the last, as I will discuss later). So what's all the disagreement about? Much of it centers on how to control the spread of the virus. Since the virus is transmitted by social interactions, it seems to follow logically that its spread will be reduced, and ultimately brought under control, by imposing, or requesting, that people restrict these interactions in various ways. There are scientists, however, who challenge the necessity and/or effectiveness of some of these measures. Since these measures require some hardship and sacrifice by the public, it's unsurprising that many lay people who object to these sacrifices will cite these scientists as a reason for not having to make them. Many of these same people also tend to believe the virus is less dangerous and deadly than the majority regards it, and also find support for this view in the work of some scientists. This view, I think, is often used as a sort of backup plan. That is, the argument is that policies imposed to reduce transmission don't work, but even if they did, they're not worth it, because the seriousness of COVID-19 is greatly exaggerated. The result is a minority, but a substantial and outspoken one, that holds the following views in opposition to the majority.
This belief system is not monolithic. For example, some scientists who believe lockdowns don't work support the use of facemasks. Some who reject facemasks accept that COVID-19 is worse than the seasonal flu. Most scientists accept the official figures of deaths and cases. But all these beliefs tend to be held together by non-scientists who reject the mainstream view, and who believe that this view is motivated by political goals, rather than by science. For these individuals, appealing to science not only supports these individual points, but proves that the majority of scientists, who reject these ideas, are not to be trusted. Unlike hard-core conspiracy theorists, many of whom tend to reject the institution of science entirely, this minority's quarrel is largely with individual scientists. They believe that science vindicates their views, and that most scientists know this, but are simply not being honest. In this article, I will discuss the scientific evidence bearing on the first issue: the effectiveness of lockdowns in reducing spread of the virus. This is the most politically contentious issue, given that it has enormous economic, as well as psychological, consequences. I plan to discuss the other issues in subsequent articles. A battle of losersNobody enjoys a lockdown. Nobody wants to shelter in place. Nobody wants to be barred from eating in a restaurant, watching a movie or a baseball game, or even from just taking a walk. We are social creatures, and despite the fact that so many of us spend so much time on the internet, most of us are not designed to go long periods of time without face-to-face interactions. Lockdowns can also have massively destructive effects on a nation's or locality's economy. Many small businesses, particularly those in the service industry, like restaurants, bars, hair salons, and gyms, can't survive very long under these circumstances, and may never recover. Schools also become casualties, with younger children particularly at risk, as this is the crucial time of their lives when they learn the social skills they will need for the rest of their lives. Though lockdowns are imposed in order to save lives, their economic consequences may in fact increase mortality rates (Bianchi et al 2020). They may also have serious psychological consequences. Mental health problems are likely to be exacerbated, as manifested in an increase in suicides, domestic abuse, and drug addiction (Winkler et al 2020; Weller et al 2020; Slavova et al 2020), though most studies to date have found no effect (Wang et al 2020; Zhu et al 2020; Leske et al 2020; Kahil et al 2020; Piquero et al 2020; Teirolf et al 2020). By now, everyone is aware of these consequences or potential consequences. The reason I feel a need to emphasize them is because they make a point that should be blatantly obvious, but which is commonly (and conveniently) overlooked by lockdown opponents: advocating lockdowns is not an economically nor psychologically self-serving position. While some people, especially the poor and certain minorities, tend to suffer worse under lockdowns than others, nobody is benefiting from them in any positive sense. Lockdowns are promoted because people fear the consequences of infection, for themselves and/or for others. This fear outweighs the negative consequences of lockdowns. For those who accept the truth of that last sentence, the only reason to oppose lockdowns would be because of strong evidence that they are ineffective. To lockdown opponents, this presents a major problem. While they may sincerely believe that this strong evidence exists, they are faced with a large majority of the world community that asserts the opposite. The only way to rationalize this is to postulate that there must be some other factor involved: that scientists, and the governments whose policies are guided by them, have another agenda. And to a great many lockdown opponents, this agenda is to extend government's control over its citizens. At this point, we reach the line, not always a sharp one, between legitimate scientific evidence and sensible policies based on it, on the one hand, and anti-scientific conspiracy theories on the other. As I've already made clear, I'm not going to address the latter here. But since any scientific view of the pandemic implies certain political and social responses to it, it's all too easy for lockdown opponents to claim that proponents of lockdowns are just using science to justify pre-established policy preferences, rather than the reverse. This charge is both ironic and hypocritical, given that the political and social agenda that is promoted by opposing lockdowns is so clear and unmistakable. In other words, if we turn this into a battle of hidden, unacknowledged motives, the lockdown opponents are going to lose, badly. Strictly speaking, science doesn't, or shouldn't, tell us what political and social policies to follow in regard to the pandemic. What it can tell us is the costs—in human health and lives— of following or not following particular policies. It's up to our actions in the political sphere to weigh those costs. I believe there's a legitimate discussion to be had attempting to balance the economic and psychological downsides of lockdowns vs. the need to reduce the spread of a deadly disease. There is nothing wrong with making this kind of argument, and appealing to science for help in determining the relative weights of lockdowns vs. no lockdowns. What is more questionable, though—and to my mind, evidence that the presenter is either not fully aware of the facts, or not being fully honest—is the claim that lockdowns don't work at all. The virus is transmitted during social interactions, so it would be nonsensical to argue that if social interactions are reduced, the transmission doesn't decrease. It may not decrease as much as had been hoped or expected, and the degree of reduction may not seem to justify the economic and other consequences. But it's very difficult to see how a lockdown—assuming it's enforced—would not result in some reduction of transmission of the virus. Yet this is exactly what many lockdown opponents propose. They claim to have provided reams of data demonstrating this. Let's examine these claims.
I believe there's a legitimate discussion to be had attempting to balance the economic and psychological downsides of lockdowns vs. the need to reduce the spread of a deadly disease.
How do we measure the measures?Lockdowns are not always precisely defined, and different people may define them somewhat differently. They generally are associated with the closing of all but the most essential businesses, and restriction of movements of citizens. In the most extreme forms, full lockdowns, all citizens are confined to their homes, except for essential activities, such as buying groceries and going to the hospital. Sometimes these exceptions are even limited to just one member of a household. In this analysis, I will inevitably be discussing and comparing countries and other population centers that have not used exactly the same measures, and to the same degree. This obviously complicates any attempt to make very precise conclusions about the effects of these policies in general. The analysis is made even more difficult by the fact that these policies have frequently not been put into place on any one specific date, but over a period of time. Many governments, for example, began response to the virus by strongly advising citizens to reduce their public activity, maybe imposing a curfew. A few days or weeks later, as the pandemic became worse, schools and some businesses were closed. Closure of other businesses may have followed, along with travel restrictions. Eventually, citizens were ordered to shelter in place. In fact, even before governments imposed any restrictions, many individuals in effect imposed some on themselves. This was especially the case early in the pandemic, when not a lot was known about how serious the virus was—how easy it was to become infected, the severity of the symptoms, or the mortality rate. Many people, fearing the worst, began reducing their social activity. Some studies have shown a significant effect of these pre-lockdown, voluntary measures in reducing spread of the virus (Santamaria and Hortal 2021), and one study claimed that this effect was actually much greater than the effect of the lockdowns themselves (Meunier 2020). Another researcher has made a similar claim, that most or all of the success of reducing transmission has come from actions occurring before the lockdown, based on the timing of these effects (Stone 2020). I will address this claim further later. But for now, I'll readily agree that voluntary behavior can potentially have a significant effect in reducing transmission. Finally, I note that just because a government imposes certain restrictions on its citizens, it doesn't necessarily mean that all of them will obey the new laws. In fact, the brief history of pandemic is riddled with incidents of people not only flouting the rules, openly or in secret, but of mass protests against these rules, and lawsuits filed against the government to pressure changes in those rules. So unless the government has unusually powerful authority over its citizens, as is the case with China, but far less so in the West, any lockdown is unlikely to be totally obeyed. Virus birth control. Bearing these qualifications in mind, how do we measure the effects of lockdowns, indeed, quantify them? Researchers examine changes in a key value known as the reproduction number (R0 or Rt). This is the average number of other people that an infected person transmits the virus to. If R0 is greater than one, than the spread of the virus increases; that is, the total number of infected people increases over time. If R0 is less than one, the spread decreases; the total number of infected people decreases. An easy way to understand this concept is to recognize that the spread, or growth, of infections in a population is analogous to the growth of a population itself. If the average couple has more than two children, the population will increase; if the average couple has less than two children, the population will decrease. The reproduction number works exactly the same way, except that single individuals give birth, so to speak, to new infections, so the magic number is one, rather than two. If a lockdown—or any other attempt to reduce the spread of the virus, such as wearing masks, social distancing, washing hands regularly, and so on—is successful, it will reduce R0 to less than 1, so that the spread of the virus is decreasing. If the R0 value is maintained below 1, the virus will eventually be eradicated from the population, though how long this takes depends on how low the R0 value is that is maintained. Even if the R0 value does not fall below 1, though, if it's decreased significantly from its original value, the lockdown or other mitigation measure can be considered to be somewhat effective, in that it has reduced the number of infections—and in the case of the coronavirus, deaths—that otherwise would have occurred. As we will see later, this is an important point that's often overlooked by lockdown critics. There have been a large number of studies that have shown that lockdowns have indeed reduced R0, very frequently to levels well below 1 (Al Zobbi et al 2020; Caristia et al 2020; Di Domenico et al 2020; Hyafil et al. 2020; Mitra et al 2020; Peirlinck et al 2020; Rost et all 2020). These studies have been carried out on a diverse number of nations, including the U.S., many countries in Europe, India and China, among others. A little later, I will describe some examples of these effects, showing—in a simplified manner—how we come to these conclusions from easily available public data. That being the case, how can anyone claim that lockdowns don't work? The short answer is that most lockdown opponents ignore these studies, if they are even aware of them, and focus on other evidence. Some lockdown opponents, as I have already alluded to earlier, argue that the effects attributed to lockdowns may have resulted from other actions. Another argument is that the reduction in transmission of the virus is not that great. Lockdown opponents also cite examples of countries that had lockdowns to no apparent effect, and conversely, countries that succeeded in bringing the virus under control without a lockdown. What I'm going to do here is examine some of this other evidence, and the arguments based on it. Buy high, sell lowOne approach used by those who oppose lockdowns is to compare the average number of daily cases—positive tests for the virus—during periods when lockdowns are in place, vs. periods when the social restrictions have been eased. Here's an example from lockdown opponent Ivor Cummins, in a podcast: 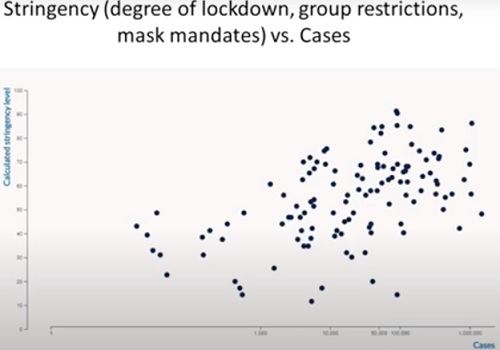
Figure 1. Daily Case Rates Don't Correlate with Degree of Social Restrictions.
The vertical axis plots some value based on degree of stringency—e.g., a total lockdown of all non-essential businesses, along with shelter in place would have a higher score than one in which only some businesses were closed, and people were free to leave their homes—vs. the horizontal plot of number of cases. The hypothesis being tested is that if lockdowns have an effect, we should see fewer daily cases associated with greater restrictions—in other words, there should be a line (with little scatter if there is a high correlation), beginning at the upper left corner of the graph (high stringency, few cases), sloping down to the bottom right corner (low stringency, many cases). Instead, there is an enormous amount of scatter—indicating relatively low correlation between the two variables—and what correlation there may be appears to be in the opposite direction, with the trend sloping from the lower left to the upper right. The conclusion is that lockdowns have no detectable effect on the spread of the virus. But there is an obvious flaw with this approach. Lockdowns are not imposed by governments randomly or arbitrarily. They're put into place specifically when case rates begin to rise, and they generally stay in place until case rates fall. Since it will take some time for the lockdown to have any effect, it will invariably be associated with very high case rates. And conversely, when the lockdown is lifted, case rates will be lower. They may rise again eventually, but this will be after some period of time, and when they do rise, more restrictions will probably be resumed. A good example of this is shown by Cummins, though he seems completely unaware that it makes this point (I have actually used a slightly different graph, available at the gov.uk website[1], because Cummins's graph is blurry, with the values very difficult to read; but the data are essentially the same):
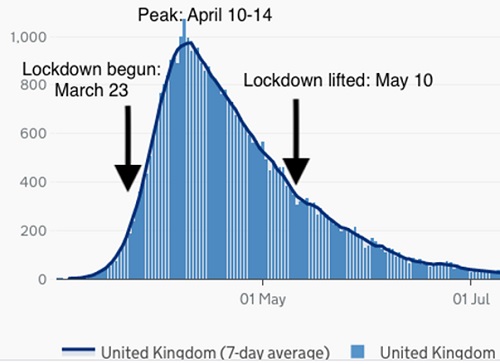
Figure 2. Daily Deaths in the UK Before, During and After Lockdown
The graph shows the daily deaths from the virus in the UK from late March until well into the summer (the actual values are represented by the vertical bars, while the 7 day moving average is given by the curve). A lockdown was imposed on March 23, indicated by the arrow on the left, and was lifted, at least to some extent, on May 10, depicted by the arrow on the right. As one can see at a glance, because the lockdown was begun when deaths were rising, of course there are going to be relatively more deaths occurring during the lockdown (portion of the graph between the two arrows). Conversely, the lockdown wasn't lifted until deaths had fallen considerably, so we would expect lower values to occur during a period when the lockdown was off (portion of graph outside both of the arrows). Deaths are often as a better way to track the spread of the virus than cases, since they have a close relationship to infections, whereas that of cases to infections is more variable. Deaths lag cases by about three weeks, though; that is, on average, people die from the virus about this length of time after testing positive. So if we were to plot cases over this time period, the curve would be shifted to the left. There would be more cases, relative to deaths, during the period preceding the lockdown, and fewer cases during the lockdown. But the point is, the nature of lockdowns is that they are always going to be associated with a lot of cases and deaths, no matter how effective they may prove to be. So attempting to show a correlation, or lack of same, between case numbers during and outside of lockdowns, it seems to me, is not a very meaningful approach. A hitch in the argumentCummins and his guest, Reid Sheftall, not only seem unaware of this, but they interpret this graph as further evidence against lockdowns. Sheftall, who is advertised as �super smart�, comments that �I can see no hitch whatsoever in this graph that corresponds to�21 days.[or any other time] that corresponds to when the lockdown was begun or when it was lifted�. It took me a long time to figure out what in the world he was talking about. Hello? About three weeks after the lockdown was begun (April 10-14), the daily deaths peak, right on schedule, and begin falling soon after. What better evidence could you want that the lockdown worked? Sheftall and Cummins apparently believe that in the absence of any social restrictions, the spread of the virus would have risen to the same peak, and declined. They seem to think that this curve represents the normal spread of the virus, so that if the lockdown had an effect on it, there would be a noticeable �hitch� in it. This is based on an idea proposed by Michael Levitt, whom Cummins has also interviewed. I will discuss it in more detail later, but for now, suffice it to say there is very little evidence in support of it, a great deal against it, and no very plausible explanation of how it could happen. There are very few scientists who would look at this graph and conclude that it showed no evidence of an effect of the lockdown. The power of a powerSo how should we view this graph? I have just pointed out that daily deaths peaked and began declining several weeks after the lockdown began, which is very strong evidence that it worked. But can we quantitate this effect? As I discussed earlier, we do it by tracking the R0 value. I will now elaborate on how we do this. We begin by asking, what would the graph look like if there were no lockdown, if the virus spread unimpeded through the population? Under these conditions, we would expect the cases and deaths to rise exponentially. That is, the number of new cases or deaths each day should be a certain, fixed percentage higher than the previous day's total. Suppose a population—a nation, a state, some community—has 1000 cases on a certain day; we'll call it day 1, though it would have been preceded by several or many other days with cases. On day 2, there are 1100 new, additional cases—an increase of 10%. In classic exponential growth, and what one would expect if the virus is spreading unimpeded, we would see another 10% increase on day 3—that is, 1210 new cases. Day 4 would have 1331 cases, and so on. Day 2: 1100 Day 3: 1210 Day 4: 1331 Day 5: 1464 Day 6: 1611 Day 7: 1772 Day 8: 1949 How do we convert data like this to a reproduction number? Epidemiologists use some complex formulas, but the basic idea is very simple. If we know how long an infected person remains infectious—capable of transmitting the virus to other people—then the increase in cases over this period of time reflects this number. Specifically, based on some studies (He et al 2020), it appears that the infectious period is about one week. This is a rough estimate, but will suffice for our purposes. From the numbers I listed above, it follows that the 1000 initial cases on Day 1 resulted in about 1950 cases on Day 8, one week later. So the reproduction number is 1950/1000 = 1.95. This is the average number of people that one infected person infects. I emphasize this is just an illustrative example, though in fact, this value is very roughly what the R0 for the coronavirus is thought to be; in the absence of social restrictions, several studies have estimated it as between 2 and 4 (Liu et al 2020; Peng et al 2020; Wang et al 2020). And as long as daily cases increase by a constant %, that value will be constant. This is a very important point that many lockdown opponents, I think, miss. If there is no effect of a lockdown, or any other attempt to slow the spread of the virus, the number of cases will continue to rise exponentially, indefinitely. If we plot the number of cases per day on a semi-log plot (logarithm of cases vs. time in days), we will see a straight line, rising from left to right, with the slope of the line representing the % daily increase: 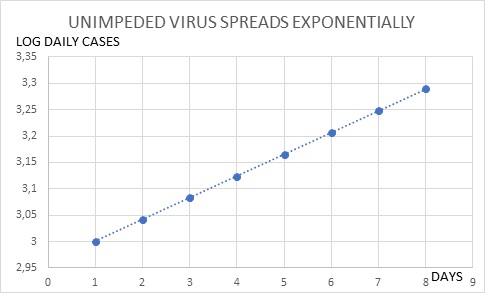
Figure 3a. When Uncontrolled, Viral Infections Increase Exponentially.
If we plot the data using standard, non-logarithmic axes, as was done in the preceding figure of UK data, the curve will be concave—the slope will continue to increase, until it approaches a vertical line. It will never reach a peak (I have assumed a 30% daily increase, to exaggerate the effect, but any % increase will give the same concave-shaped curve). 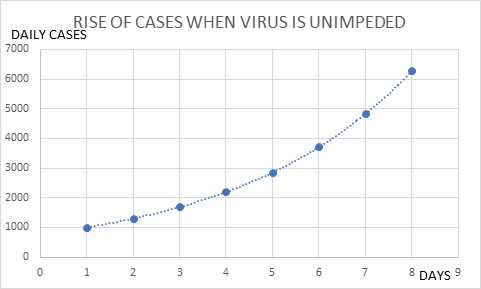
Figure 3b. When Uncontrolled, Viral Infections Increase Indefinitely.
This being the case, reducing the spread of the virus does not result in a hitch in the curve; it creates the curve. If there were no effect of a lockdown, or other restrictive measures, there would be no rise, peak and decline; there would only be a constant rise. When there is an effect on transmission, the curve is �bent�—that is, the slope constantly decreases—but this effect is not observed as a discontinuity in the curve. It bends gradually and smoothly. Are there no other factors than social restrictions that act to slow the spread of the virus? Assuming that those who become infected and recover develop long-lasting immunity (which seems to be the case, though we still don't know how long this immunity lasts), the spread will eventually begin to slow down, as fewer uninfected people remain to sustain it. When the proportion of uninfected people in the population falls to a certain critical value—1/R0—the daily number of cases will peak. At this point, herd immunity has been reached, and the presence of the virus will eventually decline, though it may take considerably more time before all infections are eradicated. But this will not occur in the relatively early phase of a pandemic, and all the data we have available indicate that no country on earth has approached herd immunity thus far. The only other well-established factor that might prematurely slow down spread of the virus is a seasonal effect. Many viral infections are known to wax and wane at periodic intervals (Fisman 2012). The familiar seasonal flu is a good example. An early study in China (Ma et al. 2020) showed that the coronavirus was slightly less deadly in higher temperatures, presumably because it is inactivated by heat. So far, though, the greatest effects on transmission of the virus have resulted from effects on human behavior. Recently, there has been a surge in cases in many countries, thought to be due to the cold weather, forcing people to spend more time indoors, where the confined space promotes spread of the virus. A similar effect was seen in the southern states of the U.S. during the summer, when very hot weather resulted in more indoor activity. While these are important observations, they emphasize the value of lockdowns in restricting the kinds of behavior that increase transmission. There is no evidence to date of seasonal changes in the virus itself that would affect its transmission, given no change in human behavior. So if lockdowns, or other social restriction measures have an effect, we will see a decrease in R0 over time. For lockdowns and similar measures to make a difference, they only need to reduce the rate of increase of cases. Cases may continue to increase, but at a lower rate. This will occur if the R0 value is reduced to a value that remains above 1. If R0 reaches 1, however, there will be a peak, and if it falls below 1, there will be a decline in cases. There is abundant evidence that this is what happens, as I will now show. The discussion that follows will not be rigorous, in that I'm using only a rough measure of R0, but it's good enough to illuminate major trends in the course of the epidemic. Readers can consult some of the studies I cited earlier for more detailed analyses. Lockdowns as takedownsHeavy liftingLike many other Americans, I blame our just departed President to some extent for not developing a unified national plan to deal with the pandemic. Instead, it was every state for itself, from acquiring personal protective equipment for doctors and nurses, to setting the rules on social activity, to testing and contact tracing. The resulting patchwork quilt of rules and regulations, however, has had one major benefit. It has created many different laboratories for testing theories about the virus, and in particular, to examine the effects of various restrictive measures. Different states have taken different approaches, with different results. Very early in the pandemic—late March and early April of 2020—most states imposed a lockdown, in which not only were most non-essential businesses closed, but citizens required to stay at home, or shelter in place, except for essential activities. Most states began re-opening in May and June, but there were great variations in what restrictions were lifted, and when. What I'm going to do here is examine six individual states. Two of them, New York (NY) and Massachusetts (MA) imposed these lockdowns until early May, at which point they began gradually rolling back these restrictions, in a series of steps. Much of this re-opening did not begin until June, however, and in NY, in particular, only some areas of the state were allowed to re-open certain businesses, depending on their daily case data. Two other states, Florida (FL) and Arizona (AZ), also imposed a lockdown, but lifted many restrictions in early May. Florida allowed restaurants and other service businesses to open at this time, though with restrictions on customer capacity. The last two states, Arkansas (AR) and Iowa (IA), did not impose lockdowns, though they did put in place some restrictive measures, such as closing schools and some businesses, and banning large assemblies of people. Table 1 shows the change in R0 values over time for each state, based on the number of daily cases. Values which were greater than 2, indicating little or no effect on daily cases, are highlighted in red/orange; values between 1 and 2, indicating daily cases were reduced, but were still increasing at the time, are highlighted in purple; and values less than one, indicating cases were decreasing, are highlighted in blue. The date the lockdown, if any, began is shown for each state.
TABLE 1. R0 VALUES IN SIX U.S. STATES FOLLOWING IMPOSITION AND LIFTING OF LOCKDOWNS
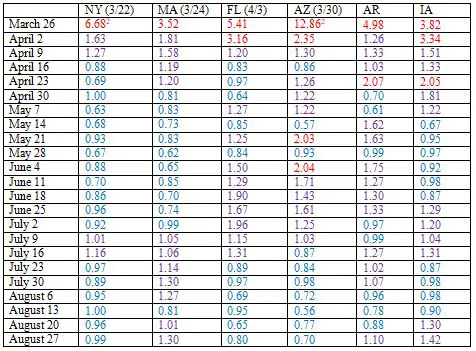 Focus first on NY and MA. The lockdowns were followed by a dramatic decrease in R0 values in both states. These values began to drop within a week or two of when the lockdown was imposed, and within several weeks had fallen well below 1. They remained below 1 for most of the summer, though there was a slight increase back over 1 in July, particularly for MA. Florida also showed a large decrease in R0 soon after the lockdown began, and the value fell below one most of the time beginning in the middle of April, and extending to the end of May. However, in early June, the value rose to well over 1, and remained at this relatively high level until near the end of July. Arizona's pattern was similar to Florida's, except that it never brought down the R0 to below 1 consistently through April and May. Beginning in June, its cases also shot up. Arkansas, one of about half a dozen states that never imposed a lockdown during this period, exhibited some decrease in R0, but it remained well above 1 for most of the summer. Iowa's R0 fell slowly at first, but eventually, beginning in the middle of May, fell slightly below 1 for several weeks, though it rose again after that. The data point to several general conclusions. First, every state with a lockdown saw a large decrease in its R0 values. These values eventually fell below 1, though in the case of FL and AZ, did not stay there long, almost surely a consequence of lifting the lockdown too soon, too fast. Even NY and MA, which were more careful, had some back-sliding. So the data show that not only do lockdowns have an effect, but that when the lockdown is halted, some or much of the effect may be reversed. Second, R0 values can certainly decrease in the absence of a lockdown. This was the case with AR and IA, both of which did impose other restrictions. But the values generally did not fall as soon or as fast, and for the most part, did not drop below 1. What about Iowa, which reported several weeks in May and June of relatively low R0 values? In early April, several thousand workers at several meat packing plants in the state tested positive for the virus, though this was not reported until May. These positives accounted for a considerable fraction of the state's total at the time. I thus speculate that they may have temporarily skewed the course of the pandemic, resulting in higher than expected R0 values earlier, and somewhat lower ones later (keep in mind that later values are based on a ratio of daily case rate to the earlier rates). In addition, when the news broke, many citizens may have taken extra precautions. In any case, weekly R0 values fluctuate randomly to a considerable extent. So it's illuminating to consider the overall drop in case rates for these six states. By the end of the summer, NY's daily case rate had fallen about 75% from what it had been on March 20, just before the lockdown was imposed, while that of MA dropped about 20-25%. In stark contrast, the case rates at the end of August for FL and AZ were about 15 times what they had been in March. For Arkansas, the factor was about 20, and for Iowa, more than 60. The lockdowns, followed by a gradual, careful re-opening, seem to have had a pronounced benefit. Surge protectionThe data I just discussed covers two major surges or waves of pandemic in the U.S. If we consider the country as a whole, there have been three such waves. The first occurred in late March and April; the second from the middle of June to about the end of July; and the third, which began in early October, is continuing today. We can track these waves by R0 values, which peak and decline, as indicated by the numbers in red (all values > 1) and blue (< 1):
TABLE 2. THREE CORONAVIRUS WAVES IN THE U.S.
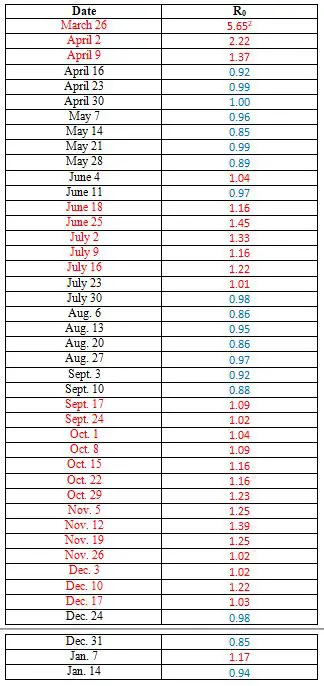 The three waves have had difference causes. The first wave was triggered by the entry into the U.S. of infected individuals from other countries where the virus was spreading, particularly Europe. Most of the cases and deaths occurred in the northeast, with New York City the epicenter. I have already pointed out the success that two states in that region, NY and MA, had with reducing R0. Notice how quickly the value was brought down to 1, and then somewhat below that. But the lockdowns were lifted, in May and June, and the result was a second wave, further evidence that lockdowns do suppress spread of the virus. Again, we saw some of this play out in the six states analyzed. Notice, though, that the R0 values never became as high as they were very early in the pandemic, in the first wave. This probably reflects, to a large degree, that people were continuing to practice social restrictions, much of them voluntarily, following the first wave. A second important observation is that the second wave lasted longer than the first. It took longer for the R0 values to be lowered to 1 and less. Why? There are probably at least two important reasons. First, local governments were slow to reinstitute lockdowns or other social restrictions, much slower than had been the case during the first wave. In fact, many states, particularly in the south and the west, where the surge in cases was highest, resisted imposing any new restrictions at all. And second, people had become weary of the social restrictions. There was a lot of ostentatious flouting of the rules—young people packing bars without wearing masks, for example. The relatively lower peak R0 values, as I just noted, suggest that many people were practicing social restrictions, but that a saturation effect had occurred. People were doing everything they could do, or were willing to do. The third wave, which began in October, appears to have been in large part the result of the coming of winter, and cold weather. People are spending more time indoors, where the virus is transmitted more easily. Much of this transmission appears to occur in homes, where most people don't wear masks, another important social restriction that I'll discuss in a future article. And two major holidays during this period, Thanksgiving and Christmas, resulted in extensive travel, and large indoor gatherings, virtually guaranteeing a surge in cases. Even so, the R0 value has fallen to below 1 again. This illustrates another important principle. The practice of social restrictions does have an effect on the virus, but when the baseline level of infections is very high, this is not apparent. The U.S. is currently experiencing its highest daily case rates and death rates since the pandemic began, despite keeping the R0 value below 1. It may appear that the practice of social restrictions is having no effect at all, but that isn't the case. The real problem—that top science advisor Anthony Fauci warned of all summer—was that case rates were not lowered when there was the chance. So now, when rates have more or less stabililized, this is of cold comfort, because they are so high. Premature death?The U.S. is just one country; let's look at some others. I'll begin with the UK. I discussed this briefly earlier, noting that a lockdown began in the UK on March 23, and was lifted, or at least, partially so, on May 10. I presented a graph of daily deaths during the period, taken from the country's website. Before going further, I want to reiterate that deaths are generally a more accurate way to track spread of the virus than cases, because they should bear a fixed relationship to infections. Cases—that is, positive tests—are certainly highly correlated with infections, but the relationship can change, particularly when the number of tests administered changes. President Trump was speaking nonsense when he said that the rise in U.S. cases last summer was due to an increase in tests, but it is true that the ratio of actual infections to cases will be affected by the number of tests. This probably accounts for some of the variation in values that I have listed so far. Tracking deaths avoids this problem, with some qualifications. The ratio of deaths to infections can also change, because of advances in treating patients, and particularly if the average age of the people infected change. Since mortality rates are much higher for older people, the ratio of deaths to infections will fluctuate according to the average or typical age of people being infected. In fact, in the U.S. there was a dramatic decrease, about 60-70%, in the CFR—case fatality rate, ratio of deaths to cases—from the first wave to the second wave, and this was mostly because the average age of people tested dropped by about ten years. But it's unlikely that the average age of people infected dropped very much, and certainly that would be unlikely to be the case over a short period of time of a few weeks. Within any wave, the ratio of deaths to infections should be fairly stable. To use deaths, however, we have to take into account a lag period. People don't die as soon as they're infected. In fact, on average, those who die do so about three weeks after testing positive; this has been a fairly consistent and accurate estimate in the U.S., and in other countries. So what do we see in the UK, following the lockdown in March? On March 29, about one week after the lockdown began, the 7 day moving average was 201. This was the average number of deaths per day during the preceding week. One week later, on April 5, it was 599, indicating an R0 of 2.99; that is, the average number of deaths during this week was three times as high as the average number of deaths during the previous week. As I noted earlier, this is a typical value for unrestrained spread of the virus. On April 13, the moving average was 916. The R0 had now dropped to 1.53, still very high, but a substantial improvement. This was about three weeks after the lockdown began, so if the lockdown worked, we would expect the R0 value to begin falling at this point. In fact, the R0 value had dropped below 1 one by April 20, and stayed well below 1 after that. Table 3 shows that a similar pattern occurred in other European nations analyzed (values highlighted by the same three-color scheme as in Table 1). All of these countries except Germany imposed a nationwide lockdown by the second or third week of March, with the exact date indicated. Germany did not have a strict lockdown, but put in various �protection� measures beginning in the second week of March. All of the countries exhibited R0 values of 2-4 or higher[2] prior to the start of the lockdown. Beginning 3-4 weeks after the lockdown started, the R0 values all began to fall, and within a few more weeks, all had dropped below 1. Italy's R0 values fell sooner than those of the other countries, in fact, within a week of when the national lockdown was imposed. This is accounted for by the fact that many strict measures were put into place in portions of the country, including Lombardy and about a dozen other provinces, several weeks ahead of the full national lockdown.
TABLE 3. EFFECT OF LOCKDOWNS ON R0 IN EUROPEAN COUNTRIES
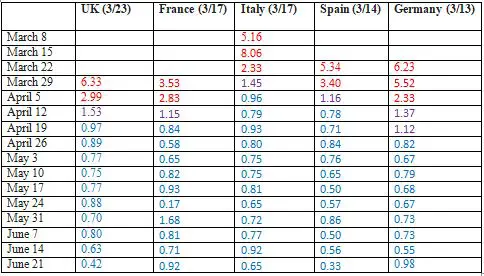 So the evidence indicates that the lockdowns had a dramatic effect in all these large European countries. Unlike the U.S., these nations did not trigger a second wave of cases and deaths when the lockdowns were eventually lifted. There was one notable European nation that did not impose a lockdown, Sweden, which is often used by lockdown opponents as an argument against that measure, but I will discuss this later. But at this time, I do want to address another argument made by a lockdown opponent. Lyman Stone (2020) has claimed that when one examines the graphs of daily deaths in certain European countries following the March lockdowns, the peak comes too soon. For example, he says that deaths peaked in Spain about 15 days, not 21 days, following the lockdown. From this he concludes that what actually caused the deaths to peak and then decline was not lockdown itself, but voluntary behavior by citizens that began several days before the lockdown. This behavior by itself, Stone argues, is sufficient. As I said before, I can certainly agree that voluntary behavior prior to a lockdown may reduce R0, particularly in the early, first wave. At that time, we didn't know how serious the virus was, and most people were inclined to assume the worst, and ready to make any sacrifice for the time being. There was not the level of skepticism about its deadliness, nor the weariness from enduring privations for long period of time, that has developed since.
So the evidence indicates that the lockdowns had a dramatic effect in all these large European countries. Unlike the U.S., these nations did not trigger a second wave of cases and deaths when the lockdowns were eventually lifted.
Note, however, that Stone is actually contradicting the title of his article, Lockdowns don't work. He's not saying they don't work. He's saying that they aren't necessary, that other measures are sufficient. His data can't possibly be used to argue that lockdowns don't work, because there is nothing people did or could have done prior to the lockdown that they weren't doing once the lockdown started. You can't, or at least wouldn't, voluntarily restrict your behavior more than it already is being restricted in a lockdown. Moreover, Stone's numbers, which he admits were preliminary at the time, look a little off to me. He says deaths in Spain reached a plateau from March 25-30, but the final records available now show the plateau occurring from March 30-April 3. That revision alone accounts for most of Stone's discrepancy. Also, if we consider cases, they peaked from March 16-20, several days after the lockdown began. Likewise, in France, another of his examples, current records indicate a plateau beginning April 2, and extending a week or more, well beyond Stone's figure of March 30-31. Cases did not peak or plateau until March 23, almost a week after the lockdown began. If there remains any doubt about the timing, I can easily offer counter-examples. As I discussed earlier, most states in the U.S. imposed lockdowns beginning in late March or early April. In most of these states, deaths peaked from 3-5 weeks after the lockdown began. Though I did not show these data in the earlier discussion, deaths peaked in NY, MA, FL and AZ at about 3, 5, 3.5 and 5 weeks, respectively, after the lockdown began. The U.S. and West Europe are developed regions, with large resources and advanced medical technologies. What about poorer, third world countries? Some of them, particularly in Southeast Asia, have actually done a better job of controlling the virus than the West, but others, notably in Latin America, have struggled more. I will consider four of these countries: El Salvador, Brazil, Argentina, and Uruguay. El Salvador is of interest, because it's often used as an example of a country that imposed severe restrictions, which seemed to have little effect on the spread of the virus. Uruguay is the opposite: it never imposed a lockdown, yet has done very well in controlling the virus (until very recently). Brazil and Argentina have much larger populations, and have struggled greatly to control the virus. Brazilian President Bolsonaro has resisted severe restrictions for the most part, but various regions in the country imposed lockdowns beginning in early May. Argentina imposed a nationwide lockdown on March 19, that was extended to May 10. Table 4 shows the changes in R0 values in these four countries, beginning in late March, and continuing to the middle of the summer. I have used daily cases rather than deaths, as two of these countries, El Salvador and Uruguay, have relatively small populations, and the numbers of deaths are not large enough to avoid considerable variability (even using cases, this is sometimes a problem. Uruguay's values are extremely volatile, because the number of cases is so small).
TABLE 4. EFFECT OF LOCKDOWN ON R0 IN LATIN AMERICAN COUNTRIES
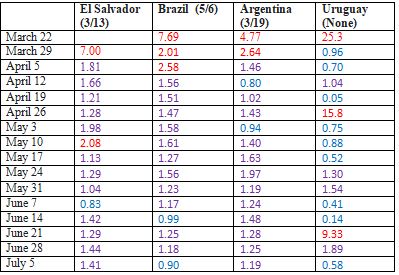 As its opponents have pointed out, the lockdown in El Salvador seemed to have little effect. The R0 values did not change much over the following months. However, there are two important qualifications to this conclusion. First, there was enormous popular resistance to the lockdown, and many people refused to comply with it. The poor are generally hurt more by lockdowns than people better off, because they need to work just to survive day to day, so one would expect less compliance in countries with a large proportion of the population living in poverty. Further exacerbating the problem, the government arrested thousands who broke quarantine, and housed them in crowded containment centers, where the virus was likely to spread even more. Second, while the lockdown began on March 13, there were no reported cases in the country until about a week later. Even after a month of being in lockdown, there had been very little spread. One might imagine the public would begin to wonder if there really was a problem to avoid, encouraging civil disobedience. Finally, while the R0 value didn't drop much for several months after the lockdown, it mostly remained in a range, 1.5-2.0, which actually indicates the spread of the virus was being slowed down. If the lockdown was having no effect at all, one would expect the R0 value to be considerably higher than this. In fact, the El Salvador numbers, along with those of the other three countries shown in the table, suggest, again, that perhaps voluntary action—and/or less restrictive measures imposed prior to the lockdown—had a significant effect in reducing R0. In none of these nations did R0 reach values as high as three. In Brazil and Argentina, the lockdowns did have a clear effect. In Brazil, the R0 had been constant at about 1.5-1.6 for almost two months, probably as a result of some moderate government actions, along with voluntary behavior. After the regional lockdowns, it dropped to about 1.2—not a major effect, but significant, considering only part of the country was locked down. Argentina's lockdown was followed by a drop of R0 from about 2.5 to 1-1.5. Uruguay, as noted earlier, has kept the virus relatively under control. This despite neighboring both Brazil and Argentina, two countries, as we have just seen, that have struggled with the virus. While there was a slow growth of case numbers, the R0 value generally stayed below 1. However, Uruguay took other measures that would have been expected to help. It shut down what we now know to be some of the worst hotspots: bars, churches and malls, along with schools. They also closed the border to Brazil. While there was no mandatory stay-at-home order, people were strongly urged to do so. And critical to the success, was a very aggressive program of testing and contact tracing. Uruguay has tested at a rate about five times higher than Argentina, and more than 100 times when the ratio of tests/positives is considered. So while the example of Uruguay may show that not all countries need a lockdown, it does suggest that countries that haven't used other aggressive measures are unlikely to benefit in the same way. Locking down by locking outI have shown that numerous analyses of lockdowns provide abundant evidence that they dramatically reduced the spread of the virus. But lockdown opponents often make the additional claim that a few countries have been able to reduce this spread without lockdowns. This is part of a larger claim, one I alluded to earlier, that the spread of the virus slows down and stops naturally or spontaneously, without any need for modification of human behavior. If this were actually the case, lockdowns would clearly be a great waste of time, money and effort. I have already discussed Uruguay in this regard, and in the discussion of individual states in the U.S., I noted that some reduction of spread was certainly achieved by measures less drastic than full lockdowns. But Sweden is the poster boy for this argument. Sweden is constitutionally barred from imposing the kind of restrictions that a lockdown entails on its citizens, yet it has consistently reported much lower case rates and mortality rates than many other European countries that imposed strict measures. So lockdown opponents constantly bring it up as a shining example that supports their argument. But there are several counter arguments to this claim. First, social restrictions have never been entirely absent from Sweden. While elementary schools have remained open, secondary schools and universities were closed early in the pandemic. While most businesses remained open, employees were urged to work at home, and about half the workforce now does so. Citizens, especially older ones, have been asked to avoid crowded areas. These measures, in turn, have had a dramatic effect on the number of people using public transportation, or simply going out and about. So it's a great exaggeration to say that in Sweden, life has gone on as normal, with no measures taken to reduce spread of the virus. Moreover, Sweden has the advantage of a low population density, a demographic that is known to correlate very highly with cases.[3] It's misleading to compare it to most other European countries, which have much higher population densities. The effect of Sweden's approach is better evaluated by comparing it to that employed by the three other Scandinavian countries it's closest to geographically, culturally, and in climate, as well as in population density. Denmark, Norway and Finland—all of which responded early and very aggressively to the pandemic, with lockdowns as well enhanced testing and contact tracing—have had case and mortality rates, per millions of people, 3-10 times lower than Sweden's. Clearly, their more restrictive approaches were more successful than Sweden's. So while we can debate how well Sweden's approach has worked—and as cases have surged recently, it appears that even the leaders of that approach have admitted some failure—Sweden does not prove that the spread of the virus can be reduced without any social restrictions, nor that restrictions beyond what Sweden has practiced have no effect. This doesn't mean nothing can be learned from the Swedish approach, but it does weaken the argument against the futility of lockdowns. Another outlier nation is Japan. Like Sweden, the government of Japan has no legal authority to impose lockdowns. All schools were closed for about a month, beginning at the end of February, and from the middle of March to early April, several measures related to a state of emergency passed. The government asked all citizens to refrain from non-essential trips out of the home. It also requested that sporting events, and other businesses involving mass audiences, be closed, while others, such as restaurants, limit their hours. Despite these relatively moderate measures, Japan has had remarkable success in reducing the spread of the virus, at least until recently. While the R0 value remained between 2-3 up until the second week in April, it dropped well below 1 after that, and has remained there until recently. Though Japan has a population more than one-third that of the U.S., even with a recent surge in cases, it has about 1% as many deaths. Japan's story is all the more remarkable in that other factors that would be thought to help control the virus have not been in its favor. As I noted earlier, population density is highly correlated with case numbers in most developed countries, yet Tokyo, along with other large cities, has one of the highest population densities in the world. Other successful countries, such as China, Iceland, Norway and South Korea, employed an aggressive testing program. Japan has tested relatively few people. So what's the secret sauce? No one really knows. Like the Chinese, the Japanese have a strong collective sense. There is strong pressure to conform to social needs. This has surely made them less resistant to requests to avoid social interactions than people in the West. The Japanese are also familiar with facemasks, as they have been used by many during the flu season in the past. But this is mostly speculation, as are other theories, such as genetic resistance to the virus. Many people have speculated that some people may be inherently resistant to infection by SARS-COV-2, and some studies suggest a role of some biochemical factors, such as blood type (Holland et al 2020). But to date, there is no evidence I'm aware of that people of certain cultures differ in their resistance to the virus, unless they may have been impacted previously by related coronaviruses. According to the CDC, case rates for Asian-Americans are roughly the same as for Caucasians.[4] Another success story that has not involved a lockdown is Hong Kong. But Hong Kong has acted very aggressively to contain the virus (Wong et al 2020), and like several other successful nations that are islands, physically or de facto—Japan, Australia, New Zealand, Taiwan, South Korea—it has been able to control influx of people into the country. Hong Kong's relatively small size also reduces the logistical problems that accompany testing and contact tracing in larger areas. So while this city's experience offers important lessons to the rest of the world, it does have advantages that other countries lack.
To conclude this discussion, there is very strong evidence that lockdowns do work�not in the sense that they will with certainty completely eradicate the virus�but that they greatly reduce its spread.
To conclude this discussion, there is very strong evidence that lockdowns do work—not in the sense that they will with certainty completely eradicate the virus—but that they greatly reduce its spread. There are exceptions, but they aren't common, and may be accounted for at least in part by other factors. Some countries have succeeded in controlling the virus while avoiding lockdowns, but all have followed some restrictions to some degree, and perhaps most important, it's not clear that the approach that worked in these countries can be successfully imported to other countries. Lowering by Levitt-atingThere remains another argument against lockdowns, one proposed by someone with impeccable scientific credentials. Michael Levitt is a Nobel Prize winner in Chemistry. While not an epidemiologist, he has a very strong familiarity with statistics and mathematical modeling, so he is not just another aging Laureate wandering into an area he knows nothing about, and embarrassing himself (James Watson, William Shockley, Brian Josephson, Kary Mullis, and many more). Levitt made a seminal observation, way back in February, when the pandemic—it technically wasn't even a pandemic then, but an epidemic—was confined to China, and mostly the province of Hubei. He found that the increase in daily cases declined. Recall the earlier discussion, when I pointed out that if a transmissible, infectious agent like a virus spreads unimpeded, we expect to observe exponential kinetics, characterized by a constant increase in the proportion of new cases. If cases increase 10% one day, they should, on average, increase by 10% the next day, by another 10% the following day, and so on. But this isn't what Levitt observed. What he found was that the % increase declined from day to day. If cases increased 10% one day, they might increase 9% the next day, 8% on the following day, and so on. As I discussed earlier, this is exactly what we expect to observe when lockdowns and other social restrictions are put into place. The R0 value, which is the ratio of new cases from one week, more or less, to those in the previous week, steadily falls. However, as the pandemic took off, and the virus spread to other nations, Levitt observed the same pattern or trend in every case. This led him to reject the idea that social restrictions could have such a universal effect. Instead, he proposed that the spread of the virus slows down, and eventually stops, naturally or spontaneously. The kind of pattern Levitt is referring to is known as a Gompertz curve, and has been applied to many biological phenomena involving growth. The basic idea is that while the initial spread of the virus, as I've emphasized, follows exponential kinetics, there is a built-in decay that results in the growth constantly slowing down, and eventually stopping entirely. Strictly speaking, mathematically the growth is governed by an exponential relationship, but the exponent is negatively correlated with the amount of growth. The Gompertz curve was initially used to model the process of death, because aging, of course, is a decay process that slows down growth and other living processes. The Gompertz equation was subsequently shown to work well for many examples of population growth, because they take place in a finite space. In this case, the decay results from overcrowding and eventually exhaustion of resources. A very well known example is exhibited by bacteria. If you seed a flask of nutrient medium with some bacteria, they will begin to reproduce immediately, and initially growth will be exponential, or �log phase�. But as the population of bacteria increases, the concentration of nutrients declines, the growth slows down, and eventually stops. The overall curve is sigmoidal, or S-shaped (Figure 4). 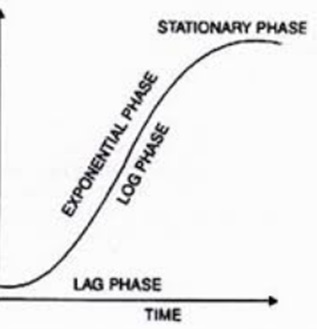
Figure 4. Gompertz Curve of Growth vs. Time
A somewhat analogous situation can be envisioned for the spread of a virus. As more and more people become infected, there are fewer uninfected people remaining—the resource or nutrient that the virus requires—so transmission is reduced. Eventually, when herd immunity is reached, the spread of the virus stops. The problem with applying this notion to the coronavirus, though, is that levels of infection are nowhere near herd immunity, and this was particularly so in the very early phase of the pandemic, when Levitt developed his theory. At this time, the pandemic was in the initial, exponential stage, when the number of uninfected people was so great that its decline over a few weeks should not have had a significant effect on the growth of cases. In Wuhan, the epicenter of the pandemic, less than one in two hundred people tested positive during the surge in January and February. A recent study using antibodies suggests that the number of infected individuals in the city was much higher—close to 5%—but this still is nowhere close to the proportion that should result in significant slowing down, let alone peaking, of cases.[5] Levitt needed another explanation for why the spread would decay. The virus did not change during this period. The virus does mutate, but most of these mutations don't affect either its transmission or its effects. Very recently, several new variants have been detected that differ from previous strains in transmissibility, but they are transmitted even more readily, not less so, which is just what one would expect (Davies et al 2020). Variants that transmit more quickly have a selective advantage over previous strains. So how does Levitt explain this natural decrease in the virus spreading? I find him very obscure on this point. He seems to think that over time, infected people run out of uninfected people to transmit the virus to. I'm not sure, but I think the idea is that our social circles overlap to a large extent, so that as the virus spreads, newly infected people have fewer other people to spread the virus to. Say you are infected with the virus, and transmit it to several other people. They might include members of your family, your workplace, and your social circle. These people, in turn, may transmit the virus to still others, but the pool is smaller. If you infect your partner, he or she can't infect you, because you already have been infected, and assuming you've recovered, have probably developed immunity to a new infection. If you infect someone where you work, that person has one less person at that place to infect. And the same with a social circle. So each infected individual operates within what is in effect a micro-environment, that results in immediate decay of growth of infections. I'm not sure this is what Levitt means—his theory also makes use of the large number of asymptomatic people—but in any case, I don't find this or any other explanation very convincing. The virus can, and will, jump out of any social circle, and infect others far away in space. Six degrees of separation, and all that. We know that virtually every country on earth has taken action to restrict activity that is thought to propagate the virus, and that large numbers of people have acted voluntarily, out of fear for themselves, as well as out of respect for others. I have pointed out studies that suggest that this pre-lockdown behavior has an effect on the transmission of the virus. That being the case, I see no reason to postulate an alternative explanation—one that seems to have no evidence to support it that isn't explained more easily and more credibly by these restrictions. I do need to emphasize that Gompertz's equations have been applied with some success by a number of researchers to modeling and predicting the spread of COVID (Catala et al 2020; Yue et al 2020; Bartolomeo et al 2021). But in this work, social restrictions aren't ignored; on the contrary, they're assumed to create the decay factor. That is, researchers look at the actual curves of cases and deaths, adjust parameters to fit them to a Gompertz equation, and based on these parameters, project how the curves will develop in the future. The approach is somewhat analogous to forecasting the stock market based on technical, rather than fundamental, factors. One looks at the actual behavior over the short-term, and without making any assumptions about what is causing this behavior, assumes that it will continue. Levitt, however, is proposing that this decay occurs even in the absence of social restrictions, which is why it appeals to opponents of lockdowns. And in addition to their not being what appears to be a very good explanation of why it should, there is also substantial evidence against Levitt's theory. The pattern he observed, in which R0 values began to fall from the beginning of the pandemic, occurred in the first wave, back in February, March and April. But subsequent events have proven that spread of the virus does not always occur in the manner that Levitt claimed. In the U.S., as I discussed earlier, there have been three major waves, in which rates of cases and deaths shot up. I listed the R0 values preceding, during and following these three waves in Table 2. The first wave, beginning in late March and starting to decline by the middle of April, did follow Levitt's description. The R0 value began dropping almost immediately after cases began to rise. But this was not the case in the second wave, occurring in June and July. The R0 value was more or less constant for 4-5 weeks before it began to fall; the same pattern can be seen in individual states that surged during the second wave, such as Florida and Arizona (Table 1). And high R0 values were sustained even longer during the third wave, for six or seven weeks. This pattern is not unique to the U.S. The UK, like many other large Europeans countries, has had two major waves, corresponding to the first and third waves in the U.S. The first wave, in March and April, like that in the U.S., was characterized by what Levitt calls �an immediate bending of the curve� (Table 3). The third wave, extending over September and October (and now resurging, perhaps because of the new variants) did not feature this bending. The R0 value was roughly constant, at about 1.5, from the middle of September to the end of October. France exhibited exponential growth for two months, over the same period, and so has Germany, beginning more recently. In fact, the most recent wave seems to be the rule regarding exponential growth, even for countries that previously had controlled the virus fairly successfully. Sweden's daily cases rose exponentially for six weeks, from the beginning of October to the middle of December. Japan's daily deaths have been rising with roughly constant R0 for the past five weeks. What are we to make of these results? Why did the first wave follow Levitt's theory, while the second and third waves did not, for a substantial period of time? Though exponential growth is characteristic of unimpeded transmission of the virus, that isn't what has been going on during this period. While the R0 values are more are less constant, they are considerably lower than the expected value of 2-4 (at least), if there were no attempts to restrict social interactions. There may be several factors, but as I discussed earlier, the most credible hypothesis is that during the first wave, everyone took social restrictions very seriously, resulting in an immediate clamping down on the spread of the virus. The second wave came after the lockdowns and other measures were lifted in much of the U.S. The governmental responses at this time were less severe than they had been in March and April, and probably even more important, if hard to document precisely, people were weary of the measures, and were less likely to adhere to them. There was also a saturation effect, seen in the fact that at the start of this second wave, the R0 value was still relatively low, and it never rose above 1.5, a value that itself was probably an outlier. People were already doing about as much as they could do, or were willing to do, keeping the R0 in the neighborhood of 1.15 � 1.25. The same is true of the third wave. The R0 never rose as high as 1.40. So the second and third waves effectively rebut Levitt's theory that the spread of the virus spontaneously or naturally slows down. Or Cummins's even vaguer claim that �it's the natural cycle that has done that itself.� In the summer in the U.S., and in the fall and early winter there and in many other places, the spread of the virus did not spontaneously slow down at first. It already had been slowed down, by human behavior, but it did not slow down further. It maintained an exponential increase for a period of several or more weeks.
So the second and third waves effectively rebut Levitt's theory that the spread of the virus spontaneously or naturally slows down. Or Cummins's even vaguer claim that “it's the natural cycle that has done that itself.”
Levitt has made other claims that, to be charitable, have not aged well. Because of his belief that the virus would slow down naturally, he predicted that overall mortality rates—the number of people who died from the virus in an entire population—would not exceed one in a thousand. That unfortunate milestone has already been reached and passed by the U.S. and about a dozen other countries, not to mention numerous states, metropolitan areas, and other municipalities. Levitt also predicted that no more than 25% of a population would become infected with the coronavirus. About than 7% of the U.S. population has tested positive to date, but based on two nation-wide antibody studies (Flower and Atchinson 2020; Bajeema et al. 2020), the total number of infected people appears to be four or five times that number.6 So America has probably already exceeded that 25% figure, with no end in sight until large numbers of people have been vaccinated. Lock down behavior, not peopleLockdowns are clearly an extreme measure, a last resort, when a contagious and for some, deadly, virus, can't be controlled. There are other, less severe restrictions—closing schools and certain businesses; banning large gatherings of people; requiring spacing among people in public; encouraging people to stay outdoors when possible; and of course, wearing masks—that may have very significant effects. The real point is to reduce the kind of behavior that transmits the virus. But as the experience in America and other countries has shown, when restrictions are lifted, and people are allowed to act �normally�, they inevitably resort to long-ingrained habits that are a boon for the virus. Lockdowns are a way of avoiding the temptation. Just as a recovering alcoholic is likely to do better by steering clear of situations in which other people are drinking, lockdowns are the surest way to lower the risk—which is why, whenever cases and deaths begin to rise, so many governments return to this tool. The development of vaccines will thankfully likely make this discussion academic eventually, ENDNOTES
REFERENCESAl Zobbi M, Alsinglawi B, Mubin O, Alnajjar F. (2020) Measurement Method for Evaluating the�Lockdown�Policies during the�COVID-19�Pandemic. Int J Environ Res Public Health. 17(15):5574. Bajema, K.M., et. Al. (2020) Estimated SARS-CoV-2 Seroprevalence in the US as of September 2020 JAMA Intern.Med. Bartolomeo N, Trerotoli P, Serio G. (2021) Short-term forecast in the early stage of the�COVID-19�outbreak in Italy. Application of a weighted and cumulative average daily growth rate to an exponential decay model. Infect Dis Model. 6:212-221 Bianchi F, Bianchi G, Song D (2020) The long-term impact of the COVID-19 unemployment shock on life expectancy and mortality rates, www.nber.org Catal� M, Alonso S, Alvarez-Lacalle E, L�pez D, Cardona PJ, Prats C. (2020) Empirical model for short-time prediction of�COVID-19�spreading. PLoS Comput Biol. Dec 9;16(12):e1008431 Caristia S, Ferranti M, Skrami E, Raffetti E, Pierannunzio D, Palladino R, Carle F, Saracci R, Badaloni C, Barone-Adesi F, Belleudi V, Ancona C (2020) Effect of national and local lockdowns on the control of�COVID-19�pandemic: a rapid review. AIE working group on the evaluation of the effectiveness of lockdowns. Epidemiol Prev. 44(5-6 Suppl 2):60-68. Davies N et al (2020) Estimated transmissibility and severity of novel SARS-CoV-2 variant of concern 2020/12-01 in England. https://cmmid.github.io/topics/covid19/uk-novel-variant.html Di Domenico L, Pullano G, Sabbatini CE, Bo�lle PY, Colizza V. (2020) Impact of�lockdown�on�COVID-19�epidemic in Ile-de-France and possible exit strategies. BMC Med. 18(1):240. Dropkin G. (2020) COVID-19�UK�Lockdown�Forecasts and R (0) Front Public Health. 8:256. Fisman (2012) Seasonality of viral infections: mechanisms and unknowns. Clin. Microbiol Infection 18, 946-954 Flower, B. and Atchinson, C. (2020) SARS-CoV-2 antibody prevalence in patients receiving dialysis in the U.S. Lancet 396, 1308-1309 He, X., et al. (2020) Temporal dynamics in viral shedding and transmissibility of COVID-19.�Nature Medicine�26: 672-675 Holland RL et al. (2020) The association of ABO blood group with indices of disease severity and multiorgan dysfunction in COVID-19. Blood Adv 4 (20): 4981-4989 Hyafil A, Mori�a D. (2020) Analysis of the impact of�lockdown�on the�reproduction�number�of the�SARS-Cov-2�in Spain. Gac Sanit. May 23:S0213-9111 Kahil K, Cheaito MA, El Hayek R, Nofal M, El Halabi S, Kudva KG, Pereira-Sanchez V, El Hayek S. (2020) Suicide�during�COVID-19�and other major international�respiratory�outbreaks: A systematic review. Asian J Psychiatr. 56:102509. Leske, S, Kolves, K, Crompton, D, Arensman, E, de Leo, D (2020) Real-time suicide mortality data from police reports in Queensland, Australia, during the COVID-19 pandemic: an interrupted time-series analysis. Lancet Psychiatry 8(1):58-63. Li Y, Wang LW, Peng ZH, Shen HB. (2020) Basic�reproduction�number�and predicted trends of�coronavirus�disease�2019�epidemic in the mainland of China. Infect Dis Poverty 9(1):94. Liu Y, Qin J, Fan Y, Zhou Y, Follmann DA, Huang CY. (2020) Estimation of infection density and epidemic size of�COVID-19�using the back-calculation algorithm. Health Inf Sci Syst. 8(1):28. Ma, Y., Zhao, Y., Liu, J., He. X., Wang, B.,Fu, S., Yan, J.,Niu,J., Sho, J., Luo, B. (2020) Effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Science of the Total Environment 724, 138226 Meuiner, T. (2020) Full lockdown policies in Western Europe countries have no evident impacts on the COVID-19 epidemic. www.medrxiv.org Mitra, A Pakhare, AP, Roy, A, Joshi, A(2020) Impact of COVID-19 epidemic curtailment strategies in selected Indian states: An analysis by reproduction number and doubling time with incidence modelling PLoS One 15(9):e0239026. Peirlinck M, Linka K, Sahli Costabal F, Kuhl E. (2020) Outbreak dynamics of�COVID-19�in China and the United States. Biomech Model Mechanobiol. 19(6):2179-2193 Peng Z, Song W, Ding Z, Guan Q, Yang X, Xu Q, Wang X, Xia Y. (2020) Linking key intervention timings to rapid declining effective�reproduction�number�to quantify lessons against�COVID-19. Front Med. 14(5):623-629. Piquero AR, Riddell JR, Bishopp SA, Narvey C, Reid JA, Piquero NL. (2020) Staying Home, Staying Safe? A Short-Term Analysis of COVID-19 on Dallas�Domestic�Violence. Am J Crim Justice. Jun 14:1-35. R�st G, Bartha FA, Bogya N, Boldog P, D�nes A, Ferenci T, Horv�th KJ, Juh�sz A, Nagy C, Tekeli T, Vizi Z, Oroszi B.(2020) Early Phase of the�COVID-19�Outbreak in Hungary and Post-Lockdown�Scenarios. Viruses 12(7):708. Russo L, Anastassopoulou C, Tsakris A, Bifulco GN, Campana EF, Toraldo G, Siettos C. (2020) Tracing day-zero and forecasting the�COVID-19�outbreak in Lombardy, Italy: A compartmental modelling and numerical optimization approach. PLoS One 15(10):e0240649. Santamar�a L, Hortal J. (2021) COVID-19�effective�reproduction�number�dropped during Spain's nationwide dropdown, then spiked at lower-incidence regions Sci Total Environ. 751:142257. Slavova S, Rock P, Bush HM, Quesinberry D, Walsh SL. (2020) Signal of increased�opioid�overdose during�COVID-19�from emergency medical services data. Drug Alcohol Depend. 214:108176. Stone, L. (2020) Lockdowns don't work. www.thepublicdiscourse.com Tierolf B, Geurts E, Steketee M. (2020) Domestic�violence in families in the Netherlands during the coronavirus crisis: A mixed method study. Child Abuse Negl. Nov 17:104800. Wang C., Pan R., Wan X., Tan Y., Xu L., McIntyre R.S., Choo F., Tran B., Ho R., Sharma V.K., Ho C. (2020) A longitudinal study on the mental health of general population during the COVID-19 Epidemic in China.�Brain Behav. Immun.�87: 40-48 Wang K, Ding L, Yan Y, Dai C, Qu M, Jiayi D, Hao X. (2020) Modelling the initial epidemic trends of�COVID-19�in Italy, Spain, Germany, and France. PLoS One 15(11):e0241743. Wang K, Zhao S, Li H, Song Y, Wang L, Wang MH, Peng Z, Li H, He D. (2020) Real-time estimation of the�reproduction�number�of the novel�coronavirus�disease (COVID-19) in China in 2020 based on incidence data Weller SJ, Tippetts D, Weston D, Aldridge RW, Ashby J. (2020) Increase in reported�domestic�abuse�in Integrated Sexual Health (ISH) services in London and Surrey during COVID-19 'lockdown': successful application of national guidance on routine enquiry during rapid transition to remote telephone consultation (telemedicine). Sex Transm Infect. Sep 22:sextrans-2020-054722. Wilasang C, Sararat C, Jitsuk NC, Yolai N, Thammawijaya P, Auewarakul P, Modchang C.J (2020) Reduction in effective�reproduction�number�of�COVID-19�is higher in countries employing active case detection with prompt isolation Travel Med. 27(5):taaa095. Winkler P, Formanek T, Mlada K, Kagstrom A, Mohrova Z, Mohr P, Csemy L. (2020) Increase in prevalence of current mental�disorders�in the context of COVID-19: analysis of repeated nationwide cross-sectional surveys. Epidemiol Psychiatr Sci. 29:e173. �� Wong MCS, Ng RWY, Chong KC, Lai CKC, Huang J, Chen Z, Boon SS, Chan PKS. (2020) Stringent containment measures without complete city�lockdown�to achieve low incidence and mortality across two waves of�COVID-19�in Hong Kong. BMJ Glob Health (10):e003573. Yue L, Tu T, Geng X. (2020) Prediction and Severity Ratings of�COVID-19�in the United States. Disaster Med Public Health Prep. Sep 10:1-9. Zhu S., Wu Y., Zhu C.Y., Hong W.C., Yu Z.X., Chen Z.K., Wang Y.G. (2020)The immediate mental health impacts of the COVID-19 pandemic among people with or without quarantine managements.�Brain Behav. Immun.�87: 56-58
|