|
TRANSLATE THIS ARTICLE
Integral World: Exploring Theories of Everything
An independent forum for a critical discussion of the integral philosophy of Ken Wilber
B. May is a former experimental high-energy particle physicist, data scientist, and business software developer.
Views from FlatlandWhat is a Theory?B. May“Physical concepts are free creations of the human mind, and are not, however it may seem, uniquely determined by the external world.” -- Albert Einstein 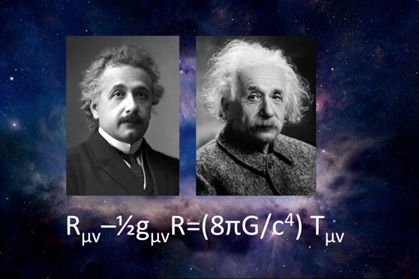
I will highlight aspects which might challenge particular claims of Ken Wilber's Integral Theory as well as the broader goal of a final and complete theory of everything.
We just celebrated the centennial of Albert Einstein's publication of his general theory of relativity, namely the theory of gravity that dethroned the previous king of celestial physics, “Newtonian” classical mechanics. In one fell swoop, “general relativity” unified matter, energy, space, and time and led to the possibility of understanding the size, shape, and evolution of the universe. The Big Bang, black holes, and gravitational lenses are just a few of its fruits that have radically changed our view of the expansive universe. Modern physics—which includes general relativity, quantum field theory, and chaos theory—is full of strange, counterintuitive, and seemingly paradoxical ideas. However, unlike the Enlightenment's scientific object-mechanical view of reality (e.g. clockworks and billiard balls)—which is still deeply ingrained in the modern Western mindset—modern physics has been met with little understanding by humanity at large. At the same time modern physics, ironically has had profound technological impacts the world over, from laser guided missiles, global positioning, and atomic reactors to ubiquitous LED televisions, mobile communications, and personal devices of all sorts. As a former experimental high-energy particle physicist, I've found that the insights, methodologies, and tools (as well as the limitations) of science and modern physics inform my views of life, the universe, and everything—including theories of everything (TOEs), grand unified theories (GUTs), and the never-ending search for holy grails of one form or another. Born and bred in scientific “flatland”, I'd like to share a variety of flatland-inspired views in a series of essays. While these views are my own and various interpretations are possible and valid, I will highlight aspects which might challenge particular claims of Ken Wilber's Integral Theory as well as the broader goal of a final and complete theory of everything. In this essay, I endeavor to distinguish “scientific theories” from other kinds of theories, explanations, and attributions for the vast mysteries that surround us, while also demonstrating that scientific theories evolve as new discoveries and new ideas come “online” in human consciousness. In the process, I hope to pay homage to Einstein and his general relativity. What Is a Scientific Theory?“It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.” — Albert Einstein Anyone can propose a theory. Indeed, humans hypothesize, deduce, adduce, and attribute "causes" and “purposes” every day, from explaining why that person cut me off in traffic to the reasons for complex international geopolitical struggles. Of course, this everyday social commentary is more reaction, judgment, or assessment based on our default world theories (worldviews) than anything resembling scientific hypothesizing. A scientific theory can be hypothesized before or after observation or experimental measurement. In either of these situations, any bias of the theorists or experimentalists (sometimes the same person) can threaten the validity of the results or conclusions, especially if it is in their interests. It is arguable that human perception and cognition is always biased in some way—if simply due to unavoidable historical, cultural, cognitive, and linguistic limitations. As such, it is left to the methodology and practices of the scientific community at large to provide systematic checks and balances. A single measurement or observation (e.g. an outlier) is not enough to confirm a hypothesis (even if hyped in the media[1]) nor is a single counter-example or negative result enough to reject an established theory (even if personally or politically advantageous). Validating or invalidating a theory takes time and the patience of a scientific community using a variety of creative experimental approaches. A “good scientific theory” is distinct from common armchair theorizing due to a set of criteria which are vetted by the scientific community over time. (These are from my personal experience, and other scientists and philosophers of science may have different or complementary views.) First, a good theory proposes a specific causal mechanism (“process”) or operating principle (“law”) at work locally, globally, or conditionally. Distinguishing an underlying process (“this follows from that because …”) from mere correlation (“this occurs with that”) is where science moves from sets of empirical data to a framework of understanding. The so-called empirical data of science does not exist as pure facts independent of some conceptual framework: although science endeavors to be “objective” (or non-subjective), it is irreducibly tied to cognition and language. In addition, science requires (an axiomatic) faith in causality—notwithstanding that Einstein himself showed that the time sequence of events is not absolute for all observers and that causality requires a “time-like” interval in space-time in which information can travel at less than the speed of light. Second, and critically, a good scientific theory is testable in three complementary ways which form the crux of the scientific process. These criteria are verifiability, falsifiability, and predictability (which of course, feeds into verifiability and falsifiability). A testable theory (hypothesis or claim) is verifiable; that is, it holds up to repeated verification with subsequent observations and measurements, even those of debunkers. Interpolations, extrapolations, and new predictions should be able to be validated again and again using a range of techniques and situations that broaden over time. Further, the theory should also be consistent and coherent with prior observations and previously validated theories—or else it should profitably subsume, complement, or supplement them. Theories that get it right usually become tools in their own right for doing new things and making new things, such as shooting men to the moon (Newtonian mechanics), building transistors and lasers (quantum mechanics), and operating fission reactors and particle colliders (quantum mechanics and special relativity). Without this proof-via-application aspect, science would largely remain pure philosophy wide open to opinion and debate. A testable theory is also falsifiable; that is, it attempts to explain and predict as much as possible based on as parsimonious principles or rules as possible. Both Newton's gravity and Einstein's general relativity attempt to explain the motion of all astronomical bodies based on very simple principles. Both theories are falsifiable due to specific quantitative predictions which can be compared with celestial observations. Although Newtonian gravity has been falsified as a fundamental theory of gravity, it is still useful and predictive, and space programs still use it for orbital calculations. Finally, a testable theory is predictive for values of measurable quantities that haven't yet been explained or observed; that is, can it fill in a hole we know exists (e.g. deviations in Mercury's orbit) or can it point to something as yet unobserved that might exist (e.g. gravitational waves)? As we will see, both Newtonian mechanics and general relativity made predictions that were confirmed and thus are both good, testable theories. Obvious or subtle deviations between observation and theory are the bleeding edge of science: did we observe something new (e.g. a new object[2] or new physics[3]) or did we make a mistake, or both? The Measure of a Theory“You have been weighed on the scales and found wanting.” — Daniel 5:27 The testability of scientific theories relies heavily (but not exclusively) on quantifiable observations using standardized measures and rigorous statistical procedures. Without reproducible quantitative standards and practices, science would remain a hodgepodge of incommensurable measurements and disparate theories with little to tie them together. At the same time, every quantitative measurement is uncertain due to intrinsic device limitations, experimental constraints, and irreducible statistical variations. Even if a predicted phenomenon seems to be observed (e.g. the Higgs boson at the Large Hadron Collider), a majority of analysis goes into dotting the i's and crossing the t's, namely, making sure that the measured “signal” is not simply due to a similar but entirely different process[4], instrumental error, or noise (which occurs in many different forms). Getting these wrong (e.g. a false positive or misinterpretation of results like cold fusion) can be not only embarrassing for the investigators, but also disruptive as other scientists try to make sense of the results, perhaps launching their own investigations.

Figure 1: Hubble Ultra-Deep Field image containing about 10,000 previously unknown galaxies.
The quantitative nature of science gives it a unique power to discriminate between competing theories. If the measurements are vague and uncertain (poorly measured or based on human perception or opinion), they admit a wider range of theories since there is less discernable detail, behavior, or structure to explain: any theory that fits within the data's uncertainty range cannot be clearly excluded or falsified. Measurement precision is equivalent to “resolving power”, that is, the ability distinguish finer and finer details. When pointed at a so-called dark region of sky, the Hubble telescope resolves thousands of previously unknown galaxies, some estimated to be 13 billion years old (figure above) thus allowing better tests of cosmological models (e.g. big bang theory). If light from the sun is passed through a prism and measured with a high resolution detector, the spectrum resolves details such as absorption lines of molecules near the sun's surface (figure below) as well as a rising-and-falling distribution similar to quantum black-body radiation, both of which can be used to deduce composition and certain dynamics of the sun.
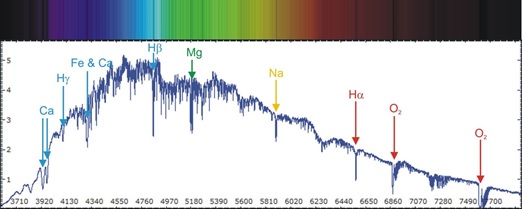
Figure 2: Visible light spectrum of the sun. Atomic/molecular absorption lines (dark lines, top) correlate with significant dips in the energy at those frequencies corresponding to specific elements and molecules in the sun. The overall rising-and-falling spectrum (bottom) is close to the radiation of a quantum mechanical “black body” at 5800 K.
At the opposite extreme, the breadth or range of observations is another type of discriminator between theories. The wider the explored domain, the more difficult it is for any theory to explain. Invariably there will be a domain or situation in which a model breaks down or reaches its predictive limits. Newtonian mechanics reaches its limit for strong gravitational fields and a variety of other situations. Black holes push both general relativity and quantum field theory to their limits, and a consistent description within both theories has challenged the likes of Steven Hawking for years. Is there new physics here (e.g. a holographic principle or multiverse), or is it a realm which in the separate views of general relativity and quantum mechanics simply cannot be squared? Other recent examples, like dark matter and dark energy, are new entries on the scene that have challenged current astrophysical and cosmological theories and our assumptions about the constituency of matter in the universe. Of course many theories do not involve precision measurements of specific phenomena but rather a large set of correlated observations, such as plate tectonics and the theory of evolution, and these are indeed connected via sedimentary deposits and the fossil record. Sedimentary and fossil dating techniques produce a set of timelines which can be correlated and arranged in a progression giving us an aggregate historical record across the planet. Measured continental drift on the order of a couple centimeters per year actively demonstrates plate tectonics. Selective breeding (e.g. dogs, crops) and genetic engineering actively demonstrate the mechanisms of evolution—although many questions remain. These theories can be comprehensively verified via a variety of phenomena, both past and present.
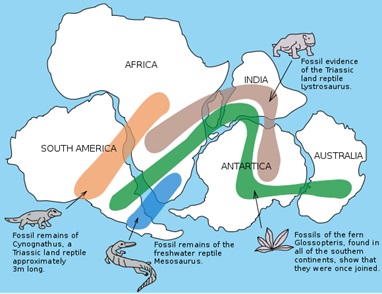
Figure 3: Illustrative fossil evidence for plate tectonics and the single continent Pangea.
It is the comprehensive and sometimes exacting criteria coupled with an ever growing volume of systematic tests and cross-checks to which scientific theories are subjected that weeds out the duds from more useful theories. (Notice I didn't say a more “real” or “true” theory. It may be more accurate, more predictive, and more informative, but absolute truth and reality are philosophical legacies which some are wont to stamp onto science—or any favored philosophy.) Many attempts have been made to firmly ground scientific knowledge upon some underlying formal axiomatic, ontological, or epistemological foundation, but these have generally confused matters, rather than let science simply speak for itself as a fruitful, evolving branch of human activity. Newton Versus Einstein“I was sitting in a chair in the patent office at Bern when all of the sudden a thought occurred to me: If a person falls freely he will not feel his own weight. I was startled. This simple thought made a deep impression on me. It impelled me toward a theory of gravitation.” — Albert Einstein

Figure 4: An “Einstein ring” of a distant blue galaxy caused by its light being bent around the central (closer) red galaxy.
Before Einstein's general relativity, the mystery of Mercury's slightly wonky orbit around the sun puzzled astrophysicists equipped with extremely successful Newtonian theory of gravity. Newtonian gravitational mechanics with clever perturbative orbital corrections very accurately predicted almost all planetary orbits. In fact, the mathematician Le Verrier predicted Neptune's existence within 1 degree based on slight discrepancies in Uranus's orbit. It was only a matter of someone pointing his telescope at the predicted spot to confirm Neptune's existence. Laplace, known as the “French Newton”, was so convinced in deterministic reality described by classical mechanics he concluded that given the conditions of the universe at any point in time, “nothing would be uncertain and the future just like the past would be present.” In Newtonian Mechanics, Mercury's slight orbital deviation clearly indicated to Le Verrier and others a missing planet situated between Mercury and the sun, called Vulcan. Various astronomers claimed sightings of Vulcan but unfortunately none of them could be independently confirmed. Even without proof of Vulcan's existence, the Royal Astronomical Society awarded Le Verrier a medal declaring, “Mercury is without a doubt perturbed in its path by some planet or by a group of asteroids as yet unknown”[5]. In the early twentieth century, Einstein put his general relativity to the task and proved to himself that Mercury's orbit could entirely be accounted for within general relativity due to the sun's near field influence on Mercury—a feature not present in Newtonian mechanics. Thus the Newtonian mathematical planet was kicked out of the solar system with Einstein's mathematical space-time. While Newtonian theory had predicted a new object to account for the observations, general relativity postulated a new geometry of space-time which subsumed and reframed Newtonian mechanics as a whole—Newtonian mechanics became an approximation or limiting case of general relativity. To date, general relativity has passed all its tests with flying colors[6], and easily visible demonstrations can be seen in gravitational lensing (e.g. Einstein rings), atomic clocks at different elevations or in orbit (orbiting GPS clocks must be corrected for this effect), and orbital decays of close orbiting binary stars (below). Thanks to Einstein, what we now call gravity is seen as an extensive field connecting space, time, mass, energy, and the maximum speed of travel or causality (speed of light). Today, one frequently says that a massive object like the sun “causes” gravity, but this is a misconception, a holdout from object-oriented thinking. The phenomenon we call gravity is a convenient name for a localized area of space-time curvature, but general relativity is more subtle and complex, as we will see. Paradoxically, gravity cannot be detected by an observer freely accelerating under its influence[7]. This is a consequence of curved space-time in which gravitational objects simply move along so-called geodesics of space-time (unless otherwise affected, for example by a collision). The only reason we feel gravity on earth is due to the pressure pushing up on our feet resisting our natural downward motion in curved space-time. A free-falling skydiver is weightless and experiences no “force” until air resistance (collision with air molecules) slows his acceleration to a constant terminal velocity.
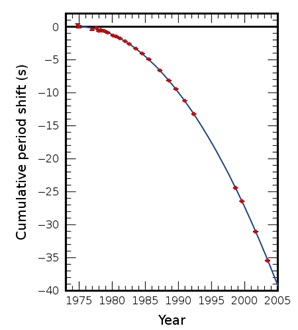
Figure 5: The gravitational orbital decay of a binary pulsar system PSR B1913+16. The measured decay (red points) and predicted decay from general relativity (blue line) differ by 0.2%.[8]
The orbital decay of closely orbiting massive objects (such as binary stars in figure above) is another observed feature of gravitational space-time that cannot be explained in the “objects plus interactions” picture of classical mechanics. Similar to quantum electrodynamics (another field theory) in which electrons forced to move in curves radiate light and lose energy, interacting gravitational bodies also lose energy by radiating space-time gravity waves (figure below)—although gravity waves have yet to be directly observed[10]. This is a unique feature of the relativistic field nature of general relativity that does not exist in a strictly object-oriented view of gravity.

Figure 6: A two-dimensional representation of gravity waves radiating out at the speed of light from an orbiting system.
Another less known feature of gravity is that two massive bodies in orbit (one “heavy” such as the sun, one “light” such as a planet) have five geometrical locations called Lagrange points for which the gravitational (attractive) and inertial (repulsive) forces are balanced (figure below, left). Low-mass objects like asteroids and dust can collect and swirl within and among these points being dragged along the orbit of the smaller orbiting body (e.g. planet). The Sun-Jupiter subsystem ushers a society of thousands of co-orbiting bodies caught in the leading and trailing wakes of Jupiter called Trojans, Greeks, and Hildas[10, video: 11] (figure below, right). We also send satellites to occupy Lagrange points[12] due to their semi-stable nature and ability to hitch a ride with the Earth's orbit, such as the Gaia astrometry observatory at the Sun-Earth's L2 point[13].
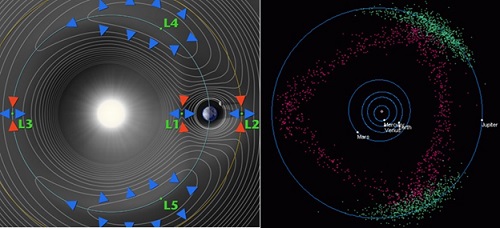
Figure 7: (Left) Effective gravitational contours of the Sun-Earth system showing the five Lagrange Points (L1-L5) which are orbital balance points accompanying a planet's orbit. (Right) Example objects that tag along Jupiter's orbit: the green dots at L4 are so-called Trojans and those at L5 are Greeks, while the red dots are Hildas which orbit in a 3:2 orbital resonance with Jupiter.
Unlike the view proposed by Newtonian mechanics and the Enlightenment, we see that law of gravity neither belongs to any single object (nor pair of objects), nor does its effect lie on a direct line between objects, nor does it act instantaneously. Rather, any moving distribution of matter behaves like a wave disturbance in space-time. In Einstein's view, modern field theories, including general relativity, defy the notion of objects or points connected by forces:[14] First of all, it was the introduction of the field concept . . . as an independent, not further reducible fundamental concept. As far as we are able to judge at present the general theory of relativity can be conceived only as a field theory. It could not have developed if one had held on to the view that the real world consists of material points which move under the influence of forces acting between them. General relativity has thus shifted our picture of gravity from a localized object-interactional view to an extensive relational-field view. Similarly, quantum field theory has changed our view from “hard point particles” to quantum wave states transforming within a dynamic energy field. Although I haven't discussed it here, chaos theory shows that a variety of emergent, dynamic arrangements (so-called attractors) can arise in a wide variety of situations, environments, and contexts. In light of these insights, Integral Theory's primary focus on self-contained stacks of holons (and collections of thereof) appears to privilege well-delimited structures over extensive contextual aspects which both transcend and irreducibly impact structure itself[15]. The Wonders of Winding Down“The 'paradox' is only a conflict between reality and your feeling of what reality 'ought to be.'" — Richard Feynman Einstein's insight of space-time as a malleable four-dimensional manifold caused a revolution in understanding the possible origin of the universe. General relativity allows for an evolving (expanding and/or contracting) space-time geometry of the universe as a whole. Edwin Hubble demonstrated an expanding visible universe, and from the view point of general relativity, the universe is now seen an expanding whole of space-time with matter being stretched out along with it. Because the universe is expanding, it has been cooling (now at a frigid 2.7 Kelvin) and condensing into quantum micro-clumps (such as nucleons, electrons, atoms, and molecules) and gravitational macro-clumps (such as stars, planetary systems, galaxies, and galaxy clusters).
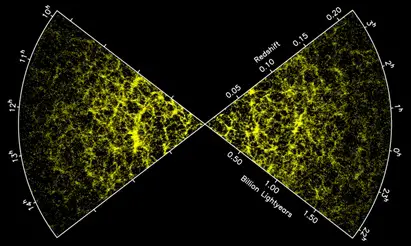
Figure 8: Large scale extra-galactic structure showing clusters and filaments.
Without gravity, space would remain essentially a rarified amorphous gas cooling and thinning out over time. However, add the attractive field of gravity, and areas of higher matter density become local minima (basins of gravity-space-time) into which matter is accelerated, leading to a dynamic balance of motion (e.g. linear and angular momentum) and potential energy (gravity). Add repulsive electromagnetism and Pauli exclusion, and aggregate astronomical objects stop collapsing, finding another balance. Add the quantum weak and strong nuclear forces, and in stars a new balance is struck resulting in a cascade of stable nuclei produced in the process (e.g. helium, oxygen, carbon, and iron). Thus structure is a combination of movement and forces finding particular balances, which may be stable like the sun and our inner solar system, or chaotic like Saturn's rings and the Kuiper belt. Emergent behavior/structure frequently arises at the localized intersection of the fundamental forces. Variations in the amounts and types of specific ingredients along the homogeneity-heterogeneity spectrum lead to varieties of emergent behavior such as diverse stellar lifecycles with end states ranging from electron-degenerate white dwarfs to neutron-degenerate pulsars to black holes.
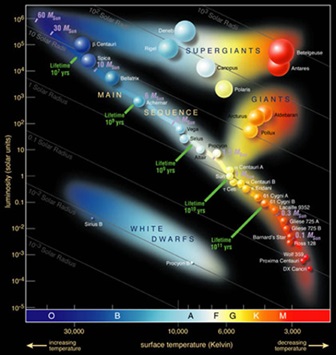
Figure 9: Schematic of main star types. It is predicted that the sun will eventually expand and become a red giant before consuming all of its fuel and becoming a white dwarf.
The sun and its orbiting sub-societies did not form independently, nor in an orderly progression[16]. Gas and other matter in the vicinity of about two light years of the sun engaged in a rotating, swirling, chaotic dance of slow accretions and hard collisions, near misses and abrupt fragmentations, and after billions of years we have our now familiar configuration: sun, four inner rocky planets, asteroid belt[17], four gaseous outer planets, Pluto and the plutinos (part of the larger Kuiper belt), and a likely huge population of objects outside the solar system proper[2,18].
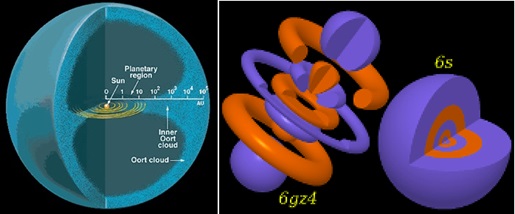
Figure 10: (Left) Schematic of the likely distribution of matter surrounding the sun two light years in radius. Note the exponential scale: the planets are within an extremely tight radius of the sun, while the “Oort cloud” extends 10,000 times further out, a similar ratio as atomic nuclei and outer electron orbits (right).
Paradoxically, although the objects (holons) in the universe become more complex and variegated in their structural arrangements, this comes with an overall winding down of usable free energy and motion. Clumps, structures, and various densities of matter form over a wide range of size (subatomic to extragalactic) and time scales (femtoseconds to billions of years) due to energetically favored bound states[19], resonances[20], and basins of attraction[21] observed throughout physical systems. Stars, galaxies, nuclei, and molecules form as energetically preferred states, and once stuck are harder to unstick. Across the board there are asymmetric processes favoring clumpy configurations over a long time. As we gaze outward or downward we see the complex “holonic” debris of a very long and sometimes tumultuous process. Looking beyond clumpy visible matter, an extremely smooth distribution of light permeates the observable universe called cosmic microwave background (CMB) radiation. The frequency distribution of the CMB behaves like radiation from a heated black body as described by quantum mechanics. Strikingly, the CMB distribution fits an ideal black body spectrum of 2.7 Kelvin (near absolute zero) within 1 part in 10,000, providing additional evidence for a Big Bang and an evolutionary picture of the universe. From this evidence, the universe overall is winding down, although local heating and “winding up” does occur, for example in stars.
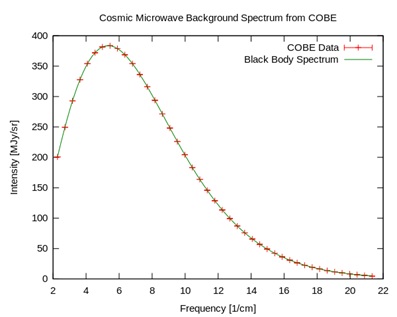
Figure 11: Observed light spectrum from the Cosmic Background Explorer (COBE) satellite (red crosses) compared with an ideal black-body spectrum (green line) at 2.7 Kelvin.
This multiple-scale evolutionary view of the universe illustrates that drawing boundaries around any object or class of objects (holons) privileges observable structure over multi-level dynamical forces at work, forces which sometimes act over very long time scales. Similarly, describing evolution as a more-or-less sequential winding-up process (as in Wilber's holarchical development) oversimplifies the messy heterogeneity and chaos involved in dynamical emergence. In the modern physics view, fields and structures, waves and particles, motion and stasis, and chaos and order are irreducible “halves” of an evolving whole, from tiny quanta to large-scale cosmology. “Beautiful” Theories“It doesn't make any difference how beautiful your guess is, it doesn't make any difference how smart you are, who made the guess, or what his name is. If it disagrees with experiment, it's wrong. That's all there is to it.” — Richard Feynman

Figure 12: Beautiful geometry of string theory.
When I was a graduate student at the University of Arizona trying to decide what I wanted to do, a middle-aged guy sporting an impressive beard (decades before hipster beards became popular) came into the physics building looking for someone to read his scientific paper, a neatly hand-written mathematical exposition on the masses of certain particles such as the electron, proton, and neutron. He had devised a scheme using the Pythagorean Theorem along with certain other fundamental constants to demonstrate the interrelated masses of these particles. However, once I spied a few arbitrary unexplained numbers interspersed throughout his equations, it was hard to take seriously as a theory. I recently found a similar kind of numerological analysis entitled "Pythagorean Geometry and Fundamental Constants"[22]. The author calculates a variety of fundamental physical constants using a range of mathematical constants and relations. Using three different methods he is able to calculate Planck's constant to eight decimal places matching the then measured (2006) value exactly. One method is shown here:
 The author concludes: From these calculations we have shown how the Pythagorean Table/Cosmological Circle encodes the harmonic compositions of four fundamental physical constants, the electron mass, and proton mass. . . . These results support the ancient view of “mandala" as an archetypal scale model of the universe, from the atom to the solar system, and beyond; part of the “cosmic canon of order, harmony, and beauty". A mandala is often defined as a “map of the cosmos". Unfortunately, the author's painstaking work is falsified by the latest measured (2014) value for Planck's constant which differs in the last four digits. While the author's attempt to derive fundamental physical constants from a range of mathematical constants and relations seems rather ambitious, his “theory” is quantifiable and thus falsifiable. But it fails as a scientific theory because it doesn't describe a specific mechanism or well-specified operating principle (as opposed to a broad, metaphorical “mandalic” principle). Nor is it coherent, predictive, parsimonious, or reproducible: it appears to require the author himself to construct just the right combinations of numbers. In 1979 Richard Feynman described the pervasive numerological penchant to “explain” the famous quantum fine-structure constant, whose reciprocal is close to 137:[23] The first idea was by Eddington, and experiments were very crude in those days and the number was very close to 136. So he proved by pure logic that it had to be 136. Then it turned out that experiment showed that it was a little wrong—it was nearer 137. So he found a slight error [in] the logic and proved with pure logic that it had to be exactly the integer 137. [But] it's not[an] integer. It's 137.0360. It seems to be a fact that's not fully appreciated by people who play with arithmetic . . . how close you can make an arbitrary number by playing around with nice numbers like pi and e. And therefore, throughout the history of physics there are paper after paper of people who have noticed that certain specific combinations give answers which are very close in several decimal places to experiment—except that the next [measured] decimal place of experiment disagrees with it. So it doesn't mean anything. Okay? Because mathematics is very powerful in the sciences and cool in its own right (to an impassioned minority), it tends to get elevated as having a fundamental mystical existence. Many math believers commit the common logical fallacy “with this, therefore because of this”: the physical universe can be explained using mathematics, therefore the universe exists because of mathematics (mathematics is fundamental). Einstein said that the “reason why mathematics enjoys special esteem, above all other sciences, is that its laws are absolutely certain and indisputable, while those of other sciences are to some extent debatable and in constant danger of being overthrown by newly discovered facts.”
 String theory is another one of those beautiful mathematical theories that has attracted attention from physicists for decades with very few (verifiable or falsifiable) predictions to show for it[24]. The believers continue their quest, while the disillusioned lament decades of wasted of effort and lack of productive results[25,26,27,28]. String theory is so flexible (“greedy”) that there are as many as 10100 possible solutions[29], one of which might correspond to our universe. Physics Nobel Laureate Melvin Schwartz lamented a future when theoretical physics could devolve to mysticism: “Unfortunately, we are rapidly approaching the time at which these theoretical notions will cease to be testable by means of experiment. When that day arrives we will find that our theorists have become the priests in what, for better or worse, has become a mythology rather than a science.” As perceptual, cognitive beings we can't help but find patterns, theories, and explanations—whether mathematical, metaphysical, or metaphorical—and make personal meaning from those patterns. Yet in the long run, science, perhaps more than any other human activity, is largely indifferent to our impulses to make ultimate conclusions about reality, meaning, and ourselves.
 Theory as Evolving Narrative“Science alone of all the subjects contains within itself the lesson of the danger of belief in the infallibility of the greatest teachers of the preceding generation.” — Richard Feynman
The larger lesson from natural science is not that it becomes better—more encompassing, more useful, more accurate, or more “profound”—but that it evolves.
Modern physics is the latest in a long line of theories, models, and paradigms. The earliest atomic theory proposed by the Greek philosophers Lucretius and Democritus around the fourth century B.C. postulated that matter consisted of a multitude of tiny indivisible geometrical particles in constant motion. Since then our picture of atoms has evolved from “marbles” to “pudding” to “planets” to our current quantum mechanical model consisting of wave functions—a progression that could not have been predicted, much less imagined. This kind of story has been replayed thousands of times in science for a variety of phenomena, from theories of combustion to theories of the cosmological origin of the universe.
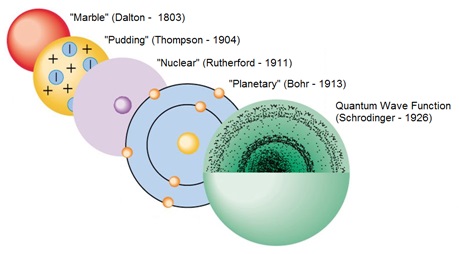
Figure 13: Evolution of atomic theories.
Although science is characterized by Wilber and others as blindly reductive, we see that science—like art, literature, and social systems—can overturn its previous attachments and limitations to find new ways to describe and unify aspects of the physical world. The table-top experiments and astronomical observations which furthered the scientific revolution were highly isolating and reductive. Yet these experiments pointed the way to integrating processes and principles such as the unification of earthly gravity and celestial mechanics (Newton), the unification of electricity and magnetism (Faraday and Maxwell), the unification of matter and energy (Einstein), the unification of causal reference frames (Einstein), and the unification of mass, space, and time (Einstein).
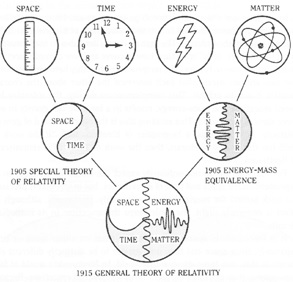
Figure 14: Schematic of a few of Einstein's theoretical contributions (unifications) and their unification within general relativity.
These principles became new knowledge usually leading to technological wonders (and horrors). But none of these pictures or models is final, complete, or “the end of physics”—a claim of scientific hubris that has been made throughout history. Albert Michelson, the first American to win a Nobel Prize in science for his precise measurements of the speed of light and disproof of the “luminiferous ether”[30], stated in 1894, “It seems probable that most of the grand underlying principles have been firmly established.” Ironically, the falsification of the ether fit with Einstein's special relativity published not long after in 1905, and the advent of quantum mechanics and general relativity shook the “firmly established” principles throughout the first half of the twentieth century. Until recently, we have been oblivious to dark matter and dark energy, and it is all but certain that we are blind to new phenomena right under our noses[31]. Science as a larger cultural phenomenon has a particular knack of breaking through and breaking down superstition, obstinacy, and hubris. What was once the unshakable dogma and truth of authority is continually eroded by constant inquiry and exploration of the world around us. Scientific knowledge evolves, whether it builds upon the previous giants or tears them down. Thus, a dominant scientific narrative, theory, or principle should neither be taken as describing the “reality”, nor as describing it, completely, once and for all. Einstein believed that epistemology of science was as important as science itself due to man's natural tendency to forget the past and reify its concepts:[32] Concepts that have proven useful in ordering things easily achieve such an authority over us that we forget their earthly origins and accept them as unalterable givens. Thus they come to be stamped as “necessities of thought,” “a priori givens,” etc. The path of scientific advance is often made impassable for a long time through such errors. For that reason, it is by no means an idle game if we become practiced in analyzing the long commonplace concepts and exhibiting those circumstances upon which their justification and usefulness depend, how they have grown up, individually, out of the givens of experience. By this means, their all-too-great authority will be broken. They will be removed if they cannot be properly legitimated, corrected if their correlation with given things be far too superfluous, replaced by others if a new system can be established that we prefer for whatever reason. Scientific “authority” can both catalyze and inhibit science's own evolution. The explosive success of Newtonian mechanics (and the calculus) boxed scientists into a corner of linear and smooth problems calculus could solve, such as the gravitational orbit of two bodies. But Newton's laws and calculus could not solve the so-called general “three-body problem”, which Henri Poincaré showed led to unpredictable motions—what we now call “chaotic”. It took clever mathematicians like Lagrange and Laplace to apply perturbation theory to Newtonian mechanics to handle with each planet's slight influence on its neighbors—although perturbative approaches miserably fail for the three or more strongly-interacting bodies and for long times. Thus our solar system is only semi-stable and ultimately chaotic in the long run. It is also no accident that the vast majority of multi-star systems are binary star systems.
Figure 15: An orbit of three (non-colliding) gravitational bodies.
In the 1970's chaos theory finally began to handle complexity in simple systems. Everyday phenomena like phase transitions between states of matter (plasma, gas, liquid, solid) and between types of behavior (e.g. laminar flow vs. turbulent flow) could now be understood in the new multi-scale paradigm of chaos theory. Likewise, the rough non-Euclidean geometry of real life—jagged mountains, irregular coastlines, branching trees and rivers, and puffy clouds—began to be framed in terms of fractal geometry advanced by Mandelbrot.

Figure 16: Part of the famed Mandelbrot set.
The larger lesson from natural science is not that it becomes better—more encompassing, more useful, more accurate, or more “profound”—but that it evolves. Unfortunately, the cultural meme of “evolution” tends to be conflated with a single-minded directional teleological purpose or goal, rather than a largely dynamical-dialectical process involving differentiations (bifurcations) and integrations (connections) across many levels.
Emergence, then, is not just a feature of the origin of species but of our very interactions, narratives, and views of nature and ourselves. Knowledge is not just categorizing and describing what we think we see, but active engagement and discovery. New “things” (e.g. dark matter, dark energy, Planet Nine, and microbiota) emerge in consciousness as do our theories and stories about them. Science, and indeed the very enterprise of life and humanity, is a continual transaction, dialogue, and negotiation with the universe—including ourselves as an irreducible element—subject to evolving possibilities, constraints, and rules of engagement we cannot completely know. Ever the modest scientist, Einstein had both humility for the human intellect and respect for the vast complexity of the universe:[33] The human mind, no matter how highly trained, cannot grasp the universe. We are in the position of a little child, entering a huge library whose walls are covered to the ceiling with books in many different tongues. The child knows that someone must have written those books. It does not know who or how. It does not understand the languages in which they are written. The child notes a definite plan in the arrangement of the books, a mysterious order, which it does not comprehend, but only dimly suspects. That, it seems to me, is the attitude of the human mind, even the greatest and most cultured, toward God. We see a universe marvelously arranged, obeying certain laws, but we understand the laws only dimly. Endnotes and References
|